|
|
|
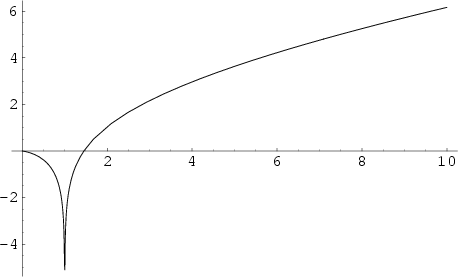
The logarithmic integral is defined by
| (1) |
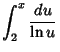 |
(2) | ||
| (3) | |||
| (4) |
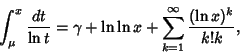 |
(5) |
![\begin{displaymath}
\int_\mu^x{dt\over\ln t}=\gamma+\ln\ln x+\sqrt{x}\sum_{n=0}^...
...}(\ln x)^n\over n!2^{n-1}}\sum_{k=0}^{[(n-1)/2]} {1\over 2k+1}
\end{displaymath}](l2_633.gif) |
(6) |
See also Polylogarithm, Prime Constellation, Prime Number Theorem, Skewes Number
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 126-131, 1994.
Nielsen, N. Theorie des Integrallogarithms. New York: Chelsea, 1965.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 151, 1991.