|
|
|
A prime constellation, also called a Prime k-Tuple or Prime k-Tuplet, is a sequence of ![]() consecutive
numbers such that the difference between the first and last is, in some sense, the least possible. More precisely, a
prime
consecutive
numbers such that the difference between the first and last is, in some sense, the least possible. More precisely, a
prime ![]() -tuplet is a sequence of consecutive Primes (
-tuplet is a sequence of consecutive Primes (![]() ,
, ![]() , ...,
, ..., ![]() ) with
) with
![]() , where
, where ![]() is the smallest number
is the smallest number ![]() for which there exist
for which there exist ![]() integers
integers
![]() ,
, ![]() and, for every
Prime
and, for every
Prime ![]() , not all the residues modulo
, not all the residues modulo ![]() are represented by
are represented by ![]() ,
, ![]() , ...,
, ..., ![]() (Forbes). For each
(Forbes). For each ![]() , this
definition excludes a finite number of clusters at the beginning of the prime number sequence. For example, (97, 101,
103, 107, 109) satisfies the conditions of the definition of a prime 5-tuplet, but (3, 5, 7, 11, 13) does not because
all three residues modulo 3 are represented (Forbes).
, this
definition excludes a finite number of clusters at the beginning of the prime number sequence. For example, (97, 101,
103, 107, 109) satisfies the conditions of the definition of a prime 5-tuplet, but (3, 5, 7, 11, 13) does not because
all three residues modulo 3 are represented (Forbes).
A prime double with ![]() is of the form (
is of the form (![]() ,
, ![]() ) and is called a pair of Twin Primes. Prime doubles of the form
(
) and is called a pair of Twin Primes. Prime doubles of the form
(![]() ,
, ![]() ) are called Sexy Primes. A prime triplet has
) are called Sexy Primes. A prime triplet has ![]() . The constellation (
. The constellation (![]() ,
, ![]() ,
, ![]() ) cannot exist,
except for
) cannot exist,
except for ![]() , since one of
, since one of ![]() ,
, ![]() , and
, and ![]() must be divisible by three. However, there are several types of prime
triplets which can exist: (
must be divisible by three. However, there are several types of prime
triplets which can exist: (![]() ,
, ![]() ,
, ![]() ), (
), (![]() ,
, ![]() ,
, ![]() ), (
), (![]() ,
, ![]() ,
, ![]() ). A Prime Quadruplet is a
constellation of four successive Primes with minimal distance
). A Prime Quadruplet is a
constellation of four successive Primes with minimal distance ![]() , and is of the form (
, and is of the form (![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
The sequence
).
The sequence ![]() therefore begins 2, 6, 8, and continues 12, 16, 20, 26, 30, ... (Sloane's A008407). Another quadruplet
constellation is (
therefore begins 2, 6, 8, and continues 12, 16, 20, 26, 30, ... (Sloane's A008407). Another quadruplet
constellation is (![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
The first First Hardy-Littlewood Conjecture states that the numbers of
constellations ![]() are asymptotically given by
are asymptotically given by
|
|
|
|
|
(1) |
|
|
|
|
|
(2) |
|
|
|
|
|
(3) |
|
|
|
|
|
(4) |
|
|
|
|
|
(5) |
|
|
|
|
|
(6) |
|
|
|
|
|
(7) |
| (8) |
The integrals above have the analytic forms
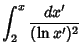 |
(9) | ||
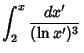 |
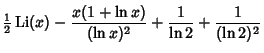 |
(10) | |
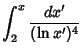 |
![$\displaystyle {1\over 6}\left\{{\mathop{\rm Li}\nolimits (x)+{2[2+\ln 2+(\ln 2)^2]\over(\ln 2)^3}-{n[2+\ln n+(\ln n)^2]\over(\ln n)^3}}\right\},$](p3_403.gif) |
(11) |
The following table gives the number of prime constellations ![]() , and the second table gives the values
predicted by the Hardy-Littlewood formulas.
, and the second table gives the values
predicted by the Hardy-Littlewood formulas.
| Count | ||||
| 1224 | 8169 | 58980 | 440312 | |
| 1216 | 8144 | 58622 | 440258 | |
| 2447 | 16386 | 117207 | 879908 | |
| 259 | 1393 | 8543 | 55600 | |
| 248 | 1444 | 8677 | 55556 | |
|
|
38 | 166 | 899 | 4768 |
|
|
75 | 325 | 1695 | 9330 |
| Hardy-Littlewood | ||||
| 1249 | 8248 | 58754 | 440368 | |
| 1249 | 8248 | 58754 | 440368 | |
| 2497 | 16496 | 117508 | 880736 | |
| 279 | 1446 | 8591 | 55491 | |
| 279 | 1446 | 8591 | 55491 | |
|
|
53 | 184 | 863 | 4735 |
|
|
Consider prime constellations in which each term is of the form ![]() . Hardy and Littlewood showed that the number
of prime constellations of this form
. Hardy and Littlewood showed that the number
of prime constellations of this form ![]() is given by
is given by
| (12) |
![\begin{displaymath}
C=\prod_{\scriptstyle p>2\atop \scriptstyle p{\rm\ prime}}\left[{1-{(-1)^{(p-1)/2}\over p-1}}\right]=1.3727\ldots
\end{displaymath}](p3_419.gif) |
(13) |
Forbes gives a list of the ``top ten'' prime ![]() -tuples for
-tuples for
![]() .
The largest known 14-constellations are
(
.
The largest known 14-constellations are
(
![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),
(
![]() , 2, 6, 8, 12, 18, 20, 26, 30, 32, 36, 42, 48, 50).
, 2, 6, 8, 12, 18, 20, 26, 30, 32, 36, 42, 48, 50).
The largest known prime 15-constellations are
(
![]() , 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56),
(
, 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56),
(
![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),
(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),
(
![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),
(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),
(
![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),
(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),
(
![]() , 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56).
, 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56).
The largest known prime 16-constellations are
(
![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),
(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),
(
![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),
(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),
(
![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),
(13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73).
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),
(13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73).
The largest known prime 17-constellations are
(
![]() , 6, 8, 12, 18, 20, 26, 32, 36, 38, 42, 48, 50, 56, 60, 62, 66),
(17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83)
(13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79).
, 6, 8, 12, 18, 20, 26, 32, 36, 38, 42, 48, 50, 56, 60, 62, 66),
(17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83)
(13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79).
See also Composite Runs, Prime Arithmetic Progression, k-Tuple Conjecture, Prime k-Tuples Conjecture, Prime Quadruplet, Sexy Primes, Twin Primes
References
Forbes, T. ``Prime
Guy, R. K. ``Patterns of Primes.'' §A9 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 23-25, 1994.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 38, 1983.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 60-74, 1994.
Sloane, N. J. A. Sequence
A008407
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
![]() -tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.
-tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.
|
|
|
© 1996-9 Eric W. Weisstein