|
|
|
The twin primes constant ![]() is defined by
is defined by
![$\displaystyle \prod_{\scriptstyle p>2\atop\scriptstyle p{\rm\ prime}} \left[{1-{1\over(p-1)^2}}\right]$](t_2501.gif) |
(1) | ||
![$\displaystyle \sum_{\scriptstyle p\geq 3\atop\scriptstyle p{\rm\ prime}}\ln\left[{p(p-2)\over (p-1)^2}\right]$](t_2503.gif) |
|||
![$\displaystyle \sum_{\scriptstyle p\geq 3\atop\scriptstyle p{\rm\ prime}} \left[{\ln\left({1-{2\over p}}\right)-2\ln\left({1-{1\over p}}\right)}\right]$](t_2504.gif) |
|||
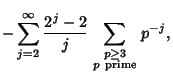 |
(2) |
|
|
(3) |
|
|
(4) |
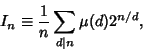 |
(5) |
The most accurately known value of ![]() is
is
| (6) |
See also Brun's Constant, Goldbach Conjecture, Mertens Constant
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/hrdyltl/hrdyltl.html
Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996.
http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Ribenboim, P. The Book of Prime Number Records, 2nd ed. New York: Springer-Verlag, p. 202, 1989.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, p. 147, 1991.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 61-66, 1994.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 30, 1993.
Wrench, J. W. ``Evaluation of Artin's Constant and the Twin Prime Constant.'' Math. Comput. 15, 396-398, 1961.
|
|
|
© 1996-9 Eric W. Weisstein