|
|
|
The first of the Hardy-Littlewood Conjectures. The ![]() -tuple conjecture states that the asymptotic number of Prime
Constellations can be computed explicitly. In particular, unless there is a trivial divisibility
condition that stops
-tuple conjecture states that the asymptotic number of Prime
Constellations can be computed explicitly. In particular, unless there is a trivial divisibility
condition that stops ![]() ,
, ![]() , ...,
, ..., ![]() from consisting of Primes infinitely often, then such Prime
Constellations will occur with an asymptotic density which is computable in terms of
from consisting of Primes infinitely often, then such Prime
Constellations will occur with an asymptotic density which is computable in terms of ![]() , ...,
, ...,
![]() . Let
. Let
![]() , then the
, then the ![]() -tuple conjecture predicts that the number of Primes
-tuple conjecture predicts that the number of Primes ![]() such that
such that
![]() ,
, ![]() , ...,
, ..., ![]() are all Prime is
are all Prime is
| (1) |
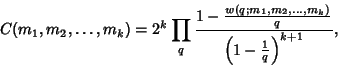 |
(2) |
| (3) |
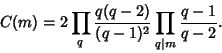 |
(4) |
This conjecture is generally believed to be true, but has not been proven (Odlyzko et al. ). The following special case of the
conjecture is sometimes known as the Prime Patterns Conjecture. Let ![]() be a Finite set of
Integers. Then it is conjectured that there exist infinitely many
be a Finite set of
Integers. Then it is conjectured that there exist infinitely many ![]() for which
for which
![]() are
all Prime Iff
are
all Prime Iff ![]() does not include all the Residues of any
Prime. The Twin Prime Conjecture is a special case of the prime patterns conjecture with
does not include all the Residues of any
Prime. The Twin Prime Conjecture is a special case of the prime patterns conjecture with ![]() . This
conjecture also implies that there are arbitrarily long Arithmetic Progressions of
Primes.
. This
conjecture also implies that there are arbitrarily long Arithmetic Progressions of
Primes.
See also Arithmetic Progression, Dirichlet's Theorem, Hardy-Littlewood Conjectures, k-Tuple Conjecture, Prime Arithmetic Progression, Prime Constellation, Prime Quadruplet, Prime Patterns Conjecture, Twin Prime Conjecture, Twin Primes
References
Brent, R. P. ``The Distribution of Small Gaps Between Successive Primes.'' Math. Comput. 28, 315-324, 1974.
Brent, R. P. ``Irregularities in the Distribution of Primes and Twin Primes.'' Math. Comput. 29, 43-56, 1975.
Halberstam, E. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1974.
Hardy, G. H. and Littlewood, J. E. ``Some Problems of `Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes.''
Acta Math. 44, 1-70, 1922.
Odlyzko, A.; Rubinstein, M.; and Wolf, M. ``Jumping Champions.''
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 66-68, 1994.
|
|
|
© 1996-9 Eric W. Weisstein