|
|
|
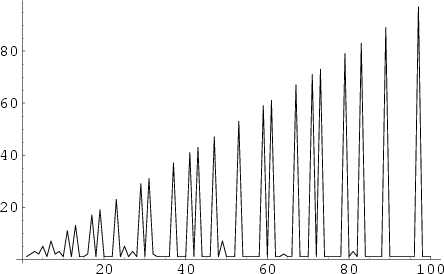
The function defined by
| (1) |
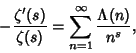 |
(2) |
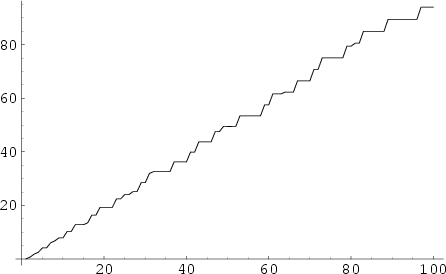
The Summatory Mangoldt function, illustrated above, is defined by
| (3) |
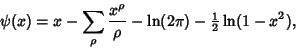 |
(4) |
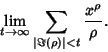 |
(5) |
| (6) |
Vallée Poussin's version of the Prime Number Theorem states that
| (7) |
| (8) |
See also Bombieri's Theorem, Greatest Prime Factor, Lambda Function, Least Common Multiple, Least Prime Factor, Riemann Function
References
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, p. 110, 1980.
Sloane, N. J. A. Sequence
A014963
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 146-147, 152-153, and 249, 1991.
|
|
|
© 1996-9 Eric W. Weisstein