|
|
|
Define
| (1) |
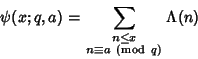 |
(2) |
| (3) |
| (4) |
| (5) |
References
Bombieri, E. ``On the Large Sieve.'' Mathematika 12, 201-225, 1965.
Davenport, H. ``Bombieri's Theorem.'' Ch. 28 in Multiplicative Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 161-168, 1980.