|
|
|
Counts the number of Positive Integers
less than or equal to a number ![]() which are not divisible by any of the first
which are not divisible by any of the first ![]() Primes,
Primes,
| (1) |
|
|
|
|
|
|
|
|
(2) |
Legendre's formula satisfies the Recurrence Relation
| (3) |
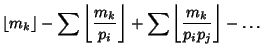 |
|||
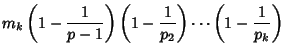 |
|||
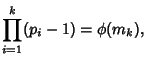 |
(4) |
| (5) |
| (6) |
Note that ![]() is not practical for computing
is not practical for computing ![]() for large arguments. A more efficient modification is
Meissel's Formula.
for large arguments. A more efficient modification is
Meissel's Formula.
See also Lehmer's Formula, Mapes' Method, Meissel's Formula, Prime Counting Function