|
|
|
A modification of Legendre's Formula for the Prime Counting Function ![]() . It starts with
. It starts with
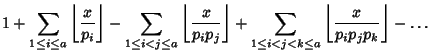 |
|||
| (1) |
| (2) |
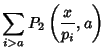 |
|||
![$\displaystyle \sum_{i=a+1}^c \sum_{j=i}^{\pi(\sqrt{x/p_i})}\left[{\pi\left({x\over p_ip_j}\right)-(j-1)}\right].$](m_889.gif) |
(3) |
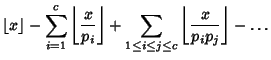 |
|||
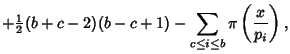 |
(4) |
| (5) | |||
| (6) |
See also Legendre's Formula, Lehmer's Formula, Prime Counting Function
References
Riesel, H. ``Meissel's Formula.'' Prime Numbers and Computer Methods for Factorization, 2nd ed.
Boston, MA: Birkhäuser, p. 12, 1994.