|
|
|
The Riemann integral is the Integral normally encountered in Calculus texts and used by physicists and engineers. Other types of integrals exist (e.g., the Lebesgue Integral), but are unlikely to be encountered outside the confines of advanced mathematics texts.
The Riemann integral is based on the Jordan Measure, and defined by taking a limit of a Riemann Sum,
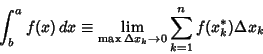 |
(1) |
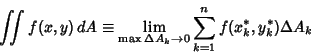 |
(2) |
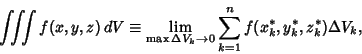 |
(3) |
As an example of the application of the Riemann integral definition, find the Area under the curve ![]() from 0 to
from 0 to
![]() . Divide
. Divide ![]() into
into ![]() segments, so
segments, so
![]() , then
, then
| (4) | |||
| (5) | |||
| (6) |
| (7) |
| (8) |
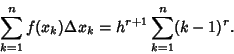 |
(9) |
|
|
|
|
|
|
|
|
(10) |
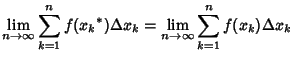 |
|||
![$\displaystyle \lim_{n\to \infty} h^3 \left[{{n(n+1)(2n+1)\over 6} - 2 {n(n+1)\over 2} + n}\right]$](r_1473.gif) |
|||
![$\displaystyle a^3 \lim_{n\to \infty} \left[{{n(n+1)(2n+1)\over 6n^3} - {n(n+1)\over n^3} + {n\over n^3}}\right]$](r_1474.gif) |
|||
| (11) |
See also Integral, Riemann Sum
References
Kestelman, H. ``Riemann Integration.'' Ch. 2 in Modern Theories of Integration, 2nd rev. ed. New York: Dover, pp. 33-66, 1960.
|
|
|
© 1996-9 Eric W. Weisstein