|
|
|
Given Mertens Function defined by
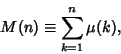 |
(1) |
| (2) |
| (3) |
Mertens conjecture was proved false by Odlyzko and te Riele (1985). Their proof is indirect and does not produce a specific
counterexample, but it does show that
| (4) |
| (5) |
It is still not known if
| (6) |
See also Mertens Function, Möbius Function, Riemann Hypothesis
References
Anderson, R. J. ``On the Mertens Conjecture for Cusp Forms.'' Mathematika 26, 236-249, 1979.
Anderson, R. J. ``Corrigendum: `On the Mertens Conjecture for Cusp Forms.''' Mathematika 27, 261, 1980.
Devlin, K. ``The Mertens Conjecture.'' Irish Math. Soc. Bull. 17, 29-43, 1986.
Grupp, F. ``On the Mertens Conjecture for Cusp Forms.'' Mathematika 29, 213-226, 1982.
Jurkat, W. and Peyerimhoff, A. ``A Constructive Approach to Kronecker Approximation and Its Application
to the Mertens Conjecture.'' J. reine angew. Math. 286/287, 322-340, 1976.
Mertens, F. ``Über eine zahlentheoretische Funktion.'' Sitzungsber. Akad. Wiss. Wien IIa 106,
761-830, 1897.
Odlyzko, A. M. and te Riele, H. J. J. ``Disproof of the Mertens Conjecture.'' J. reine angew. Math.
357, 138-160, 1985.
Pintz, J. ``An Effective Disproof of the Mertens Conjecture.'' Astérique 147-148, 325-333 and 346, 1987.
te Riele, H. J. J. ``Some Historical and Other Notes About the Mertens Conjecture and Its Recent Disproof.''
Nieuw Arch. Wisk. 3, 237-243, 1985.
|
|
|
© 1996-9 Eric W. Weisstein