The 2-1 equation
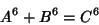 |
(1) |
is a special case of Fermat's Last Theorem with 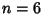 , and so has no solution. Ekl (1996) has searched and found
no solutions to the 2-2
, and so has no solution. Ekl (1996) has searched and found
no solutions to the 2-2
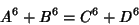 |
(2) |
with sums less than
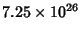 .
.
No solutions are known to the 3-1 or 3-2 equations. However, parametric solutions are known for the 3-3 equation
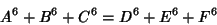 |
(3) |
(Guy 1994, pp. 140 and 142). Known solutions are
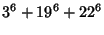 |
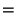 |
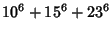 |
(4) |
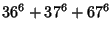 |
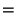 |
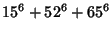 |
(5) |
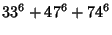 |
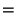 |
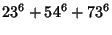 |
(6) |
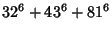 |
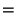 |
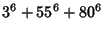 |
(7) |
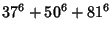 |
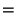 |
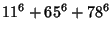 |
(8) |
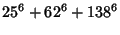 |
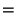 |
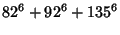 |
(9) |
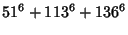 |
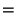 |
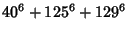 |
(10) |
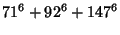 |
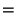 |
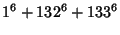 |
(11) |
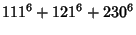 |
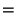 |
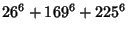 |
(12) |
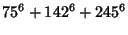 |
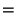 |
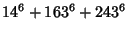 |
(13) |
(Rao 1934, Lander et al. 1967).
No solutions are known to the 4-1 or 4-2 equations. The smallest primitive 4-3 solutions are
(Lander et al. 1967). Moessner (1947) gave three parametric solutions to the 4-4 equation. The smallest 4-4 solution is
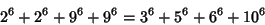 |
(19) |
(Rao 1934, Lander et al. 1967). The smallest 4-4-4 solution is
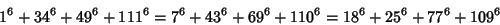 |
(20) |
(Lander et al. 1967).
No 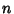 -1 solutions are known for
-1 solutions are known for 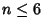 (Lander et al. 1967).
No solution to the 5-1 equation is known (Guy 1994, p. 140) or the 5-2 equation.
(Lander et al. 1967).
No solution to the 5-1 equation is known (Guy 1994, p. 140) or the 5-2 equation.
No solutions are known to the 6-1 or 6-2 equations.
The smallest 7-1 solution is
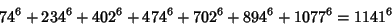 |
(21) |
(Lander et al. 1967). The smallest 7-2 solution is
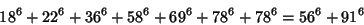 |
(22) |
(Lander et al. 1967).
The smallest primitive 8-1 solutions are
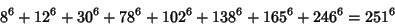 |
(23) |
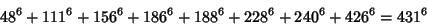 |
(24) |
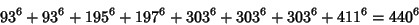 |
(25) |
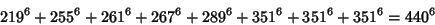 |
(26) |
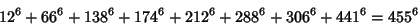 |
(27) |
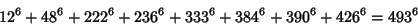 |
(28) |
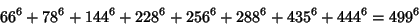 |
(29) |
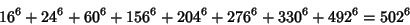 |
(30) |
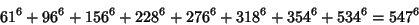 |
(31) |
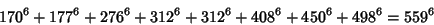 |
(32) |
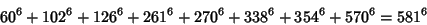 |
(33) |
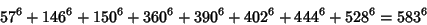 |
(34) |
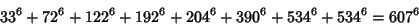 |
(35) |
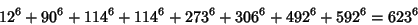 |
(36) |
(Lander et al. 1967). The smallest 8-2 solution is
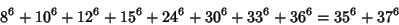 |
(37) |
(Lander et al. 1967).
The smallest 9-1 solution is
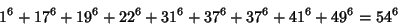 |
(38) |
(Lander et al. 1967). The smallest 9-2 solution is
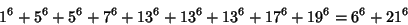 |
(39) |
(Lander et al. 1967).
The smallest 10-1 solution is
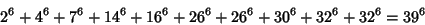 |
(40) |
(Lander et al. 1967). The smallest 10-2 solution is
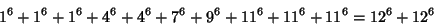 |
(41) |
(Lander et al. 1967).
The smallest 11-1 solution is
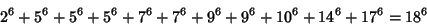 |
(42) |
(Lander et al. 1967).
There is also at least one 16-1 identity,
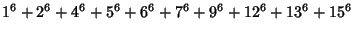
|
|
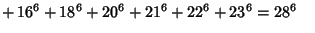
|
(43) |
(Martin 1893). Moessner (1959) gave solutions for 16-1, 18-1, 20-1, and 23-1.
References
Ekl, R. L. ``Equal Sums of Four Seventh Powers.'' Math. Comput. 65, 1755-1756, 1996.
Guy, R. K. ``Sums of Like Powers. Euler's Conjecture.'' §D1 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. ``A Survey of Equal Sums of Like Powers.'' Math. Comput.
21, 446-459, 1967.
Martin, A. ``On Powers of Numbers Whose Sum is the Same Power of Some Number.'' Quart. J. Math. 26, 225-227, 1893.
Moessner, A. ``On Equal Sums of Like Powers.'' Math. Student 15, 83-88, 1947.
Moessner, A. ``Einige zahlentheoretische Untersuchungen und diophantische Probleme.''
Glasnik Mat.-Fiz. Astron. Drustvo Mat. Fiz. Hrvatske Ser. 2 14, 177-182, 1959.
Rao, S. K. ``On Sums of Sixth Powers.'' J. London Math. Soc. 9, 172-173, 1934.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() -1 solutions are known for
-1 solutions are known for ![]() (Lander et al. 1967).
No solution to the 5-1 equation is known (Guy 1994, p. 140) or the 5-2 equation.
(Lander et al. 1967).
No solution to the 5-1 equation is known (Guy 1994, p. 140) or the 5-2 equation.