|
|
|
![]() gives the number of ways of writing the Integer
gives the number of ways of writing the Integer ![]() as a sum of Positive Integers without regard to order. For example, since 4 can be written
as a sum of Positive Integers without regard to order. For example, since 4 can be written
| (1) |
| (2) |
| 50 | 204226 |
| 100 | 190569292 |
| 200 | 3972999029388 |
| 300 | 9253082936723602 |
| 400 | 6727090051741041926 |
| 500 | 2300165032574323995027 |
| 600 | 458004788008144308553622 |
| 700 | 60378285202834474611028659 |
| 800 | 5733052172321422504456911979 |
| 900 | 415873681190459054784114365430 |
| 1000 | 24061467864032622473692149727991 |
![]() for which
for which ![]() is Prime are 2, 3, 4, 5, 6, 13, 36, 77, 132, 157, 168, 186, ... (Sloane's A046063). Numbers which
cannot be written as a Product of
is Prime are 2, 3, 4, 5, 6, 13, 36, 77, 132, 157, 168, 186, ... (Sloane's A046063). Numbers which
cannot be written as a Product of ![]() are 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, ... (Sloane's A046064),
corresponding to numbers of nonisomorphic Abelian Groups which are not possible for any group order.
are 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, ... (Sloane's A046064),
corresponding to numbers of nonisomorphic Abelian Groups which are not possible for any group order.
When explicitly listing the partitions of a number ![]() , the simplest form is the so-called natural representation
which simply gives the sequence of numbers in the representation (e.g., (2, 1, 1) for the number
, the simplest form is the so-called natural representation
which simply gives the sequence of numbers in the representation (e.g., (2, 1, 1) for the number ![]() ). The multiplicity representation instead gives the number of times each number occurs together with that number (e.g., (2, 1),
(1, 2) for
). The multiplicity representation instead gives the number of times each number occurs together with that number (e.g., (2, 1),
(1, 2) for
![]() ). The Ferrers Diagram is a pictorial representation of a partition.
). The Ferrers Diagram is a pictorial representation of a partition.
Euler ![]() invented a Generating Function which gives rise to a Power Series in
invented a Generating Function which gives rise to a Power Series in ![]() ,
,
![\begin{displaymath}
P(n)=\sum_{m=1}^\infty (-1)^{m+1} [P(n-{\textstyle{1\over 2}}m(3m-1))+P(n-{\textstyle{1\over 2}}m(3m+1))].
\end{displaymath}](p1_735.gif) |
(3) |
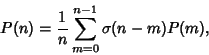 |
(4) |
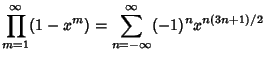 |
(5) | ||
| (6) |
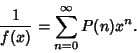 |
(7) |
| (8) |
In 1916-1917, Hardy and Ramanujan ![]() used the Circle Method and elliptic Modular Functions to obtain the approximate solution
used the Circle Method and elliptic Modular Functions to obtain the approximate solution
| (9) |
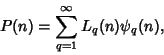 |
(10) |
| (11) | |||
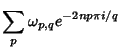 |
(12) | ||
| (13) | |||
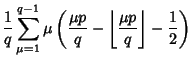 |
(14) | ||
| (15) | |||
![$\displaystyle {\sqrt{q}\over\pi\sqrt{2}}\left\{{{d\over dm} \left[{\sinh\left({K\lambda_m\over q}\right)\over\lambda_m}\right]}\right\}_{m=n},$](p1_757.gif) |
(16) |
| (17) |
With ![]() as defined above, Ramanujan
as defined above, Ramanujan ![]() also showed that
also showed that
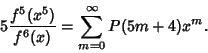 |
(18) |
| (19) |
| (20) |
| (21) |
Let ![]() be the number of partitions of
be the number of partitions of ![]() containing Odd numbers only and
containing Odd numbers only and ![]() be the number of partitions of
be the number of partitions of
![]() without duplication, then
without duplication, then
|
|
|
|
|
(22) |
Let ![]() be the number of partitions of Even numbers only, and let
be the number of partitions of Even numbers only, and let ![]() (
(![]() ) be the number of partitions
in which the parts are all Even (Odd) and all different. The first few values of
) be the number of partitions
in which the parts are all Even (Odd) and all different. The first few values of ![]() are 1, 1, 0, 1, 1, 1, 1, 1,
2, 2, 2, 2, 3, 3, 3, 4, ... (Sloane's A000700). Some additional Generating Functions are given
by Honsberger (1985, pp. 241-242)
are 1, 1, 0, 1, 1, 1, 1, 1,
2, 2, 2, 2, 3, 3, 3, 4, ... (Sloane's A000700). Some additional Generating Functions are given
by Honsberger (1985, pp. 241-242)
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
|
|
|
(27) |
|
|
(28) |
![]() , also written
, also written ![]() , is the number of ways of writing
, is the number of ways of writing ![]() as a sum of
as a sum of ![]() terms, and can be computed from the
Recurrence Relation
terms, and can be computed from the
Recurrence Relation
| (29) |
The function ![]() can be given explicitly for the first few values of
can be given explicitly for the first few values of ![]() ,
,
| (30) | |||
| (31) |
See also Alcuin's Sequence, Elder's Theorem, Euler's Pentagonal Number Theorem, Ferrers Diagram, Partition Function Q, Pentagonal Number, r(n), Rogers-Ramanujan Identities, Stanley's Theorem
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Unrestricted Partitions.'' §24.2.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 825, 1972.
Adler, H. ``Partition Identities--From Euler to the Present.'' Amer. Math. Monthly 76, 733-746, 1969.
Adler, H. ``The Use of Generating Functions to Discover and Prove Partition Identities.'' Two-Year College Math. J. 10,
318-329, 1979.
Andrews, G. Encyclopedia of Mathematics and Its Applications, Vol. 2: The Theory of Partitions.
Cambridge, England: Cambridge University Press, 1984.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 94-96, 1996.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 40-45 and 64-68, 1985.
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 237-239, 1991.
Jackson, D. and Goulden, I. Combinatorial Enumeration. New York: Academic Press, 1983.
MacMahon, P. A. Combinatory Analysis. New York: Chelsea, 1960.
Rademacher, H. ``On the Partition Function
Ruskey, F. ``Information of Numerical Partitions.''
http://sue.csc.uvic.ca/~cos/inf/nump/NumPartition.html.
Sloane, N. J. A. Sequences A000009/M0281, A000041/M0663, A000700/M0217, A001318/M1336, A046063, and A046064 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
![]() .'' Proc. London Math. Soc. 43, 241-254, 1937.
.'' Proc. London Math. Soc. 43, 241-254, 1937.
|
|
|
© 1996-9 Eric W. Weisstein