|
|
|
The Integer Sequence 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8, 12, 10, 14, 12, 16, 14, 19, 16, 21, 19,
... (Sloane's A005044) given by the Coefficients of the Maclaurin Series for
![]() . The number
of different Triangles which have Integral sides and Perimeter
. The number
of different Triangles which have Integral sides and Perimeter ![]() is given
by
is given
by
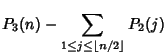 |
(1) | ||
![$\displaystyle \left[{n^2\over 12}\right]-\left\lfloor{n\over 4}\right\rfloor \left\lfloor{n+2\over 4}\right\rfloor$](a_578.gif) |
(2) | ||
![$\displaystyle \left\{\begin{array}{ll} \left[{n^2\over 48}\right]& \mbox{for $n$\ even}\\ \left[{(n+3)^2\over 48}\right]& \mbox{for $n$\ odd,}\end{array}\right.$](a_579.gif) |
(3) |
See also Partition Function P, Triangle
References
Andrews, G. ``A Note on Partitions and Triangles with Integer Sides.'' Amer. Math. Monthly 86, 477, 1979.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 39-47, 1985.
Jordan, J. H.; Walch, R.; and Wisner, R. J. ``Triangles with Integer Sides.'' Amer. Math. Monthly 86, 686-689, 1979.
Sloane, N. J. A. Sequence
A005044/M0146
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.