|
|
|
![]() gives the number of ways of writing the Integer
gives the number of ways of writing the Integer ![]() as a sum of Positive Integers
without regard to order with the constraint that all Integers in each sum are distinct. The values for
as a sum of Positive Integers
without regard to order with the constraint that all Integers in each sum are distinct. The values for
![]() , 2, ... are 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (Sloane's A000009). The Generating Function for
, 2, ... are 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (Sloane's A000009). The Generating Function for ![]() is
is
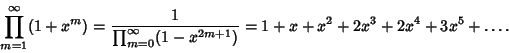
The number of Partitions of ![]() with
with ![]() summands is denoted
summands is denoted ![]() or
or
![]() . Therefore,
. Therefore, ![]() and
and
See also Partition Function P
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Partitions into Distinct Parts.'' §24.2.2 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 823-824, 1972.
Sloane, N. J. A. Sequences
A046065 and
A000009/M0281
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.