|
|
|
A power series in a variable ![]() is an infinite Sum of the form
is an infinite Sum of the form
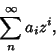 |
(1) |
A Conjecture of Pólya is that if a Function has a Power series with Integer Coefficients and Radius of Convergence 1, then either the Function is Rational or the Unit Circle is a natural boundary.
A generalized Power sum ![]() for
for ![]() , 1, ... is given by
, 1, ... is given by
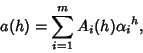 |
(2) |
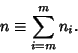 |
(3) |
For any power series, one of the following is true:
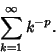 |
(4) |
See also Binomial Series, Convergence Tests, Laurent Series, Maclaurin Series, Multinomial Series, p-Series, Polynomial, Power Set, Quotient-Difference Algorithm, Recurrence Sequence, Series, Series Reversion, Taylor Series
References
Arfken, G. ``Power Series.'' §5.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 313-321, 1985.
Myerson, G. and van der Poorten, A. J. ``Some Problems Concerning Recurrence Sequences.'' Amer. Math. Monthly 102, 698-705, 1995.
Pólya, G. Mathematics and Plausible Reasoning, Vol. 2: Patterns of Plausible Inference.
Princeton, NJ: Princeton University Press, p. 46, 1954.
|
|
|
© 1996-9 Eric W. Weisstein