|
|
|
For ![]() ,
,
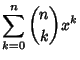 |
(1) | ||
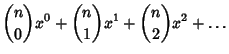 |
(2) | ||
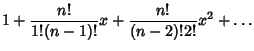 |
(3) | ||
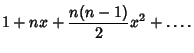 |
(4) |
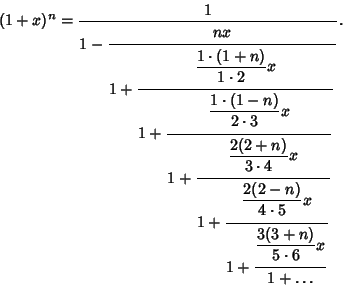 |
(5) |
See also Binomial Theorem, Multinomial Series, Negative Binomial Series
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 14-15, 1972.
Pappas, T. ``Pascal's Triangle, the Fibonacci Sequence & Binomial Formula.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 40-41, 1989.