|
|
|
Series reversion is the computation of the Coefficients of the inverse function given those of the forward function.
For a function expressed in a series as
| (1) |
| (2) |
|
|
|
|
|
|
|
|
(3) |
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) |
|
|
|
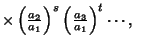
|
(11) |
where
| (12) |
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 316-317, 1985.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 297, 1987.
Dwight, H. B. Table of Integrals and Other Mathematical Data, 4th ed. New York: Macmillan, 1961.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 411-413, 1953.
|
|
|
© 1996-9 Eric W. Weisstein