Figurate Number

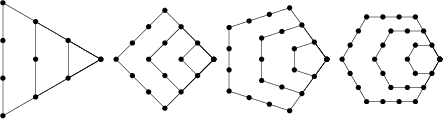
A number which can be represented by a regular geometrical arrangement of equally spaced points. If the arrangement forms a Regular Polygon, the number is called a Polygonal Number. The polygonal numbers illustrated above are called triangular, square, pentagonal, and hexagon numbers, respectively. Figurate numbers can also form other shapes such as centered polygons, L-shapes, 3-dimensional solids, etc. The following table lists the most common types of figurate numbers.

Name	Formula
Biquadratic Number
Centered Cube Number
Centered Pentagonal Number	${\textstyle{1\over 2}}(5n^2+5n+2)$
Centered Square Number
Centered Triangular Number	${\textstyle{1\over 2}}(3n^2-3n+2)$
Cubic Number
Decagonal Number
Gnomic Number
Heptagonal Number	${\textstyle{1\over 2}}n(5n-3)$
Hex Number
Heptagonal Pyramidal Number	${\textstyle{1\over 6}}n(n+1)(5n-2)$
Hexagonal Number
Hexagonal Pyramidal Number	${\textstyle{1\over 6}}n(n+1)(4n-1)$
Octagonal Number
Octahedral Number	${\textstyle{1\over 3}}n(2n^2+1)$
Pentagonal Number	${\textstyle{1\over 2}}n(3n-1)$
Pentagonal Pyramidal Number	${\textstyle{1\over 2}}n^2(n+1)$
Pentatope Number	${\textstyle{1\over 24}}n(n+1)(n+2)(n+3)$
Pronic Number
Rhombic Dodecahedral Number
Square Number
Stella Octangula Number
Tetrahedral Number	${\textstyle{1\over 6}} n(n+1)(n+2)$
Triangular Number	${\textstyle{1\over 2}}n(n+1)$
Truncated Octahedral Number
Truncated Tetrahedral Number	${\textstyle{1\over 6}} n(23n^2-27n+10)$