|
|
|
A Figurate Number ![]() of the form
of the form
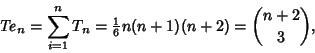 |
(1) |
| (2) |
The only numbers which are simultaneously Square and Tetrahedral are
![]() ,
, ![]() , and
, and
![]() (giving
(giving ![]() ,
, ![]() , and
, and ![]() ), as proved by Meyl
(1878; cited in Dickson 1952, p. 25). Numbers which are simultaneously Triangular and
tetrahedral satisfy the Binomial Coefficient equation
), as proved by Meyl
(1878; cited in Dickson 1952, p. 25). Numbers which are simultaneously Triangular and
tetrahedral satisfy the Binomial Coefficient equation
| (3) |
See also Pyramidal Number, Truncated Tetrahedral Number
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
Beukers, F. ``On Oranges and Integral Points on Certain Plane Cubic Curves.''
Nieuw Arch. Wisk. 6, 203-210, 1988.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 44-46, 1996.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, 1952.
Guy, R. K. ``Figurate Numbers.'' §D3 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 147-150, 1994.
Meyl, A.-J.-J. ``Solution de Question 1194.'' Nouv. Ann. Math. 17, 464-467, 1878.
Sloane, N. J. A. Sequence
A000292/M3382
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein