|
|
|
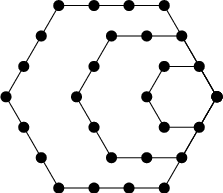
A Figurate Number and 6-Polygonal Number of the form ![]() . The first few are 1, 6, 15, 28, 45,
... (Sloane's A000384). The Generating Function of the hexagonal numbers
. The first few are 1, 6, 15, 28, 45,
... (Sloane's A000384). The Generating Function of the hexagonal numbers
Every hexagonal number is a Triangular Number since
See also Figurate Number, Hex Number, Triangular Number
References
Duke, W. and Schulze-Pillot, R. ``Representations of Integers by Positive Ternary Quadratic Forms and Equidistribution
of Lattice Points on Ellipsoids.'' Invent. Math. 99, 49-57, 1990.
Guy, R. K. ``Sums of Squares.'' §C20 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138, 1994.
Legendre, A.-M. Théorie des nombres, 4th ed., 2 vols. Paris: A. Blanchard, 1979.
Sloane, N. J. A. Sequence
A000384/M4108
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.