|
|
|
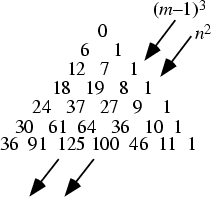
A Number Triangle created by setting the Vertex equal to 0, filling one diagonal with 1s,
the other diagonal with multiples of an Integer ![]() , and filling in the remaining entries by summing the elements on
either side from one row above. Call the first column
, and filling in the remaining entries by summing the elements on
either side from one row above. Call the first column ![]() and the last column
and the last column ![]() so that
so that
| (1) | |||
| (2) |
| (3) |
| (4) |
| (5) |
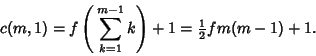 |
(6) |
| (7) |
| (8) |
![$\displaystyle \sum_{k=1}^m [{\textstyle{1\over 2}}fk(k-1)+1]=\sum_{k=1}^m({\textstyle{1\over 2}}fk^2-{\textstyle{1\over 2}}fk+1)$](c2_230.gif) |
|||
| (9) |
| (10) |
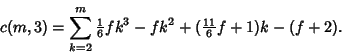 |
(11) |
| (12) |
So far, this has just been relatively boring Algebra. But the amazing part is that if ![]() is chosen as the
Integer, then
is chosen as the
Integer, then ![]() and
and ![]() simplify to
simplify to
| (13) | |||
| (14) |
See also Bell Triangle, Catalan's Triangle, Euler's Triangle, Leibniz Harmonic Triangle, Number Triangle, Pascal's Triangle, Seidel-Entringer-Arnold Triangle, Sum
References
Clark, J. E. ``Clark's Triangle.'' Math. Student 26, No. 2, p. 4, Nov. 1978.
|
|
|
© 1996-9 Eric W. Weisstein