|
|
|
Find the minimum size Square capable of bounding ![]() equal Squares arranged in any
configuration. The only packings which have been proven optimal are 2, 3, 5, and Square Numbers
(4, 9, ...). If
equal Squares arranged in any
configuration. The only packings which have been proven optimal are 2, 3, 5, and Square Numbers
(4, 9, ...). If ![]() for some
for some ![]() , it is Conjectured that the size of the minimum bounding
square is
, it is Conjectured that the size of the minimum bounding
square is ![]() for small
for small ![]() . The smallest
. The smallest ![]() for which the Conjecture is known to be violated is 1560. The
size is known to scale as
for which the Conjecture is known to be violated is 1560. The
size is known to scale as ![]() , where
, where
| Exact | Decimal | |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 2 | 2 |
| 4 | 2 | 2 |
| 5 |
|
2.707... |
| 6 | 3 | 3 |
| 7 | 3 | 3 |
| 8 | 3 | 3 |
| 9 | 3 | 3 |
| 10 |
|
3.707... |
| 11 | 3.877... | |
| 12 | 4 | 4 |
| 13 | 4 | 4 |
| 14 | 4 | 4 |
| 15 | 4 | 4 |
| 16 | 4 | 4 |
| 17 |
|
4.707... |
| 18 |
|
4.822... |
| 19 |
|
4.885... |
| 20 | 5 | 5 |
| 21 | 5 | 5 |
| 22 | 5 | 5 |
| 23 | 5 | 5 |
| 24 | 5 | 5 |
| 25 | 5 | 5 |
| 26 | 5.650... |
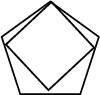
The best packing of a Square inside a Pentagon, illustrated above, is 1.0673....
References
Erdös, P. and Graham, R. L. ``On Packing Squares with Equal Squares.'' J. Combin. Th. Ser. A
19, 119-123, 1975.
Friedman, E. ``Packing Unit Squares in Squares.'' Elec. J. Combin. DS7, 1-24, Mar. 5, 1998.
http://www.combinatorics.org/Surveys/.
Gardner, M. ``Packing Squares.'' Ch. 20 in
Fractal Music, Hypercards, and More Mathematical Recreations from Scientific
American Magazine. New York: W. H. Freeman, 1992.
Göbel, F. ``Geometrical Packing and Covering Problems.'' In Packing and Covering in
Combinatorics (Ed. A. Schrijver). Amsterdam: Tweede Boerhaavestraat, 1979.
Roth, L. F. and Vaughan, R. C. ``Inefficiency in Packing Squares with Unit Squares.''
J. Combin. Th. Ser. A 24, 170-186, 1978.
|
|
|
© 1996-9 Eric W. Weisstein