Medial Triangle

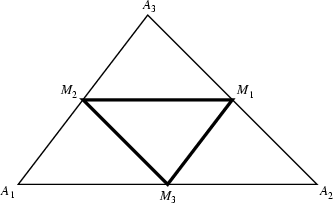
$\begin{figure}\begin{center}\BoxedEPSF{medial_triangle.epsf scaled 700}\end{center}\end{figure}$

The Triangle $\Delta M_1M_2M_3$ formed by joining the Midpoints of the sides of a Triangle $\Delta A_1A_2A_3$ . The medial triangle is sometimes also called the Auxiliary Triangle (Dixon 1991). The medial triangle has Trilinear Coordinates

$\displaystyle A'$	$\textstyle =$	$\displaystyle 0:b^{-1}:c^{-1}$
$\displaystyle B'$	$\textstyle =$	$\displaystyle a^{-1}:0:c^{-1}$
$\displaystyle C'$	$\textstyle =$	$\displaystyle a^{-1}:b^{-1}:0.$

The medial triangle $\Delta M_1'M_2'M_3'$ of the medial triangle $\Delta M_1M_2M_3$ of a Triangle $\Delta A_1A_2A_3$ is similar to $\Delta A_1A_2A_3$ .

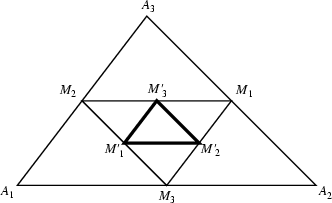
$\begin{figure}\begin{center}\BoxedEPSF{medial_triangle2.epsf scaled 700}\end{center}\end{figure}$

See also Anticomplementary Triangle

References

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 18-20, 1967.

Dixon, R. Mathographics. New York: Dover, p. 56, 1991.