|
|
|
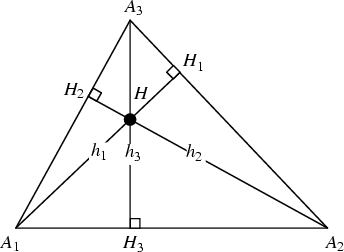
The altitudes of a Triangle are the Cevians ![]() which are Perpendicular to the
Legs
which are Perpendicular to the
Legs ![]() opposite
opposite ![]() . They have lengths
. They have lengths
![]() given by
given by
| (1) |
| (2) |
| (3) |
Other formulas satisfied by the altitude include
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
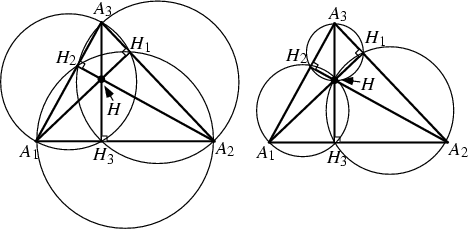
The points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (and their permutations with respect to indices) all lie on a Circle, as
do the points
(and their permutations with respect to indices) all lie on a Circle, as
do the points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (and their permutations with respect to indices). Triangles
(and their permutations with respect to indices). Triangles
![]() and
and
![]() are inversely similar.
are inversely similar.
The triangle ![]() has the minimum Perimeter of any Triangle inscribed in a given Acute Triangle
(Johnson 1929, pp. 161-165). The Perimeter of
has the minimum Perimeter of any Triangle inscribed in a given Acute Triangle
(Johnson 1929, pp. 161-165). The Perimeter of
![]() is
is ![]() (Johnson 1929, p. 191). Additional
properties involving the Feet of the altitudes are given by Johnson (1929, pp. 261-262).
(Johnson 1929, p. 191). Additional
properties involving the Feet of the altitudes are given by Johnson (1929, pp. 261-262).
See also Cevian, Foot, Orthocenter, Perpendicular, Perpendicular Foot
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 9 and 36-40, 1967.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, 1929.
|
|
|
© 1996-9 Eric W. Weisstein