|
|
|
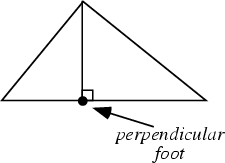
The Foot of the Perpendicular is the point on the leg opposite a given vertex of a Triangle at which the Perpendicular passing through that vertex intersects the side. The length of the Line Segment from the vertex to the perpendicular foot is called the Altitude of the Triangle.
See also Altitude, Foot, Perpendicular, Perpendicular Bisector