|
|
|
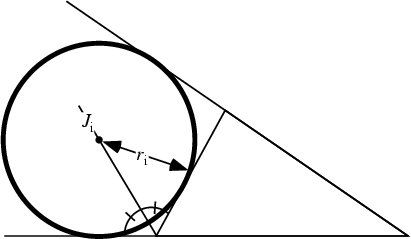
The Radius of an Excircle. Let a Triangle have exradius ![]() (sometimes denoted
(sometimes denoted ![]() ),
opposite side
),
opposite side ![]() and angle
and angle ![]() , Area
, Area ![]() , and Semiperimeter
, and Semiperimeter ![]() . Then
. Then
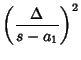 |
(1) | ||
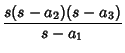 |
(2) | ||
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
See also Circle, Circumradius, Excircle, Inradius, Radius
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, 1929.
Mackay, J. S. ``Formulas Connected with the Radii of the Incircle and Excircles of a Triangle.''
Proc. Edinburgh Math. Soc. 12, 86-105.
Mackay, J. S. ``Formulas Connected with the Radii of the Incircle and Excircles of a Triangle.''
Proc. Edinburgh Math. Soc. 13, 103-104.
|
|
|
© 1996-9 Eric W. Weisstein