|
|
|
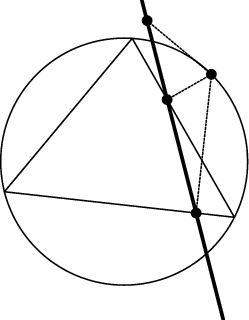
The Simson line is the Line containing the feet of the perpendiculars from a point on the Circumcircle of a Triangle to the sides (or their extensions) of the Triangle. The Simson line is sometimes known as the Wallace-Simson Line, since it does not appear in any work of Simson (Johnson 1929, p. 137).
The Angle between the Simson lines of two points ![]() and
and ![]() is half the Angle of the arc
is half the Angle of the arc ![]() . The Simson
line of any Vertex is the Altitude through that Vertex. The
Simson line of a point opposite a Vertex is the corresponding side. If
. The Simson
line of any Vertex is the Altitude through that Vertex. The
Simson line of a point opposite a Vertex is the corresponding side. If ![]() is the Simson
line of a point
is the Simson
line of a point ![]() of the Circumcircle, then the triangles
of the Circumcircle, then the triangles ![]() and
and ![]() are directly similar.
are directly similar.
See also Circumcircle
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.,
pp. 40-41 and 43-45, 1967.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 137-139, 1929.