|
|
|
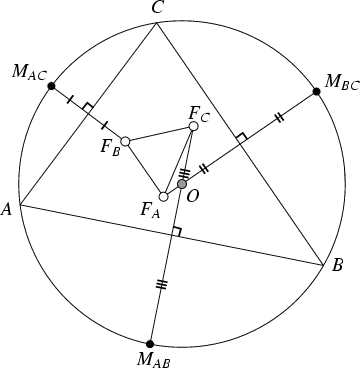
The Fuhrmann triangle of a Triangle ![]() is the Triangle
is the Triangle
![]() formed by reflecting the
Mid-Arc Points
formed by reflecting the
Mid-Arc Points ![]() ,
, ![]() ,
, ![]() about the lines
about the lines ![]() ,
, ![]() , and
, and ![]() . The
Circumcircle of the Fuhrmann triangle is called the Fuhrmann Circle, and the lines
. The
Circumcircle of the Fuhrmann triangle is called the Fuhrmann Circle, and the lines ![]() ,
, ![]() , and
, and
![]() Concur at the Circumcenter
Concur at the Circumcenter ![]() .
.
See also Fuhrmann Circle, Mid-Arc Points
References
Fuhrmann, W. Synthetische Beweise Planimetrischer Sätze. Berlin, p. 107, 1890.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 228-229, 1929.