|
|
|
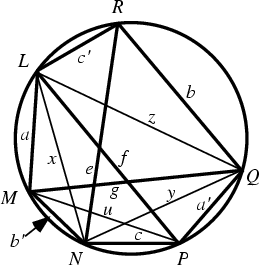
Let the opposite sides of a convex Cyclic Hexagon be ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and let the
Diagonals
, and let the
Diagonals ![]() ,
, ![]() , and
, and ![]() be so chosen that
be so chosen that ![]() ,
, ![]() , and
, and ![]() have no common
Vertex (and likewise for
have no common
Vertex (and likewise for ![]() ,
, ![]() , and
, and ![]() ), then
), then
See also Cyclic Hexagon, Hexagon, Ptolemy's Theorem
References
Fuhrmann, W. Synthetische Beweise Planimetrischer Sätze. Berlin, p. 61, 1890.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 65-66, 1929.