|
|
|
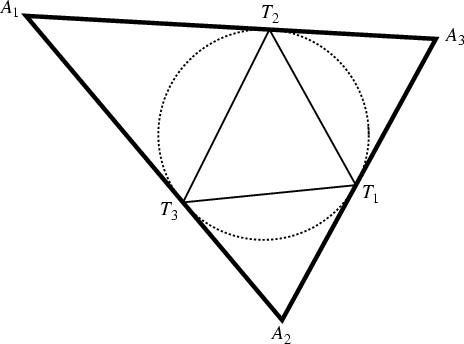
The Triangle
![]() formed by the lines tangent to the Circumcircle of a given Triangle
formed by the lines tangent to the Circumcircle of a given Triangle
![]() at its Vertices. It is the Pedal Triangle of
at its Vertices. It is the Pedal Triangle of
![]() with
the Circumcenter as the Pedal Point. The Trilinear Coordinates of the Vertices of the tangential triangle are
with
the Circumcenter as the Pedal Point. The Trilinear Coordinates of the Vertices of the tangential triangle are
See also Circumcircle, Contact Triangle, Gergonne Point, Pedal Triangle, Perspective