|
|
|
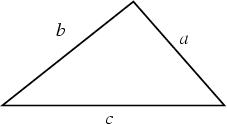
Specifying three sides uniquely determines a Triangle whose Area is given by Heron's Formula,
| (1) |
| (2) |
| (3) |
| (4) | |||
| (5) | |||
| (6) |
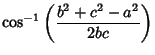 |
(7) | ||
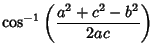 |
(8) | ||
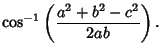 |
(9) |
See also AAA Theorem, AAS Theorem, ASA Theorem, ASS Theorem, Heron's Formula, SAS Theorem, Semiperimeter, Triangle