Let there be two functions 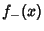 and
and 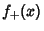 such that
such that 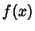 is ``squeezed'' between
the two,
is ``squeezed'' between
the two,
If
then
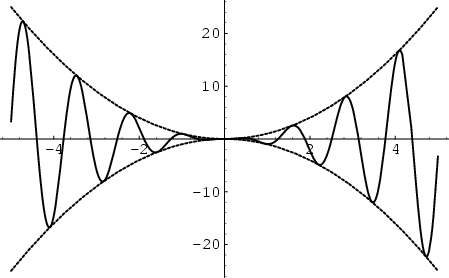
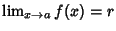 . In the above diagram the functions
. In the above diagram the functions 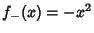 and
and 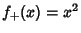 ``squeeze''
``squeeze'' 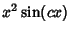 at 0, so
at 0, so
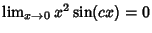 . The squeezing theorem is also called the Sandwich Theorem.
. The squeezing theorem is also called the Sandwich Theorem.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() such that
such that ![]() is ``squeezed'' between
the two,
is ``squeezed'' between
the two,