|
|
|
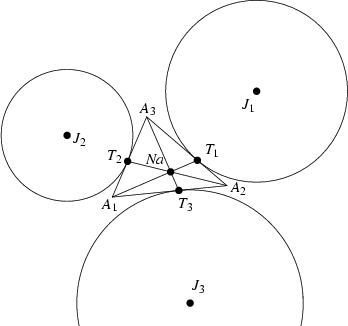
Let ![]() be the point at which the
be the point at which the ![]() -Excircle meets the side
-Excircle meets the side ![]() of a Triangle
of a Triangle ![]() , and define
, and define ![]() and
and ![]() similarly. Then the lines
similarly. Then the lines ![]() ,
, ![]() , and
, and ![]() Concur in the Nagel Point.
Concur in the Nagel Point.
The Nagel point can also be constructed by letting ![]() be the point half way around the Perimeter of
be the point half way around the Perimeter of ![]() starting at
starting at ![]() , and
, and ![]() and
and ![]() similarly defined. Then the lines
similarly defined. Then the lines ![]() ,
, ![]() , and
, and ![]() concur in the Nagel point.
It is therefore sometimes known as the Bisected Perimeter Point (Bennett et al. 1988, Chen et al. 1992, Kimberling 1994).
concur in the Nagel point.
It is therefore sometimes known as the Bisected Perimeter Point (Bennett et al. 1988, Chen et al. 1992, Kimberling 1994).
The Nagel point has Triangle Center Function
See also Excenter, Excentral Triangle, Excircle, Mittenpunkt, Trisected Perimeter Point
References
Altshiller-Court, N. College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed.
New York: Barnes and Noble, pp. 160-164, 1952.
Bennett, G.; Glenn, J.; Kimberling, C.; and Cohen, J. M. ``Problem E 3155 and Solution.'' Amer. Math. Monthly 95, 874, 1988.
Chen, J.; Lo, C.-H.; and Lossers, O. P. ``Problem E 3397 and Solution.'' Amer. Math. Monthly 99, 70-71, 1992.
Eves, H. W. A Survey of Geometry, rev. ed. Boston, MA: Allyn and Bacon, p. 83, 1972.
Gallatly, W. The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, p. 20, 1913.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 184 and 225-226, 1929.
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.
Kimberling, C. ``Nagel Point.''
http://cedar.evansville.edu/~ck6/tcenters/class/nagel.html.
|
|
|
© 1996-9 Eric W. Weisstein