|
|
|
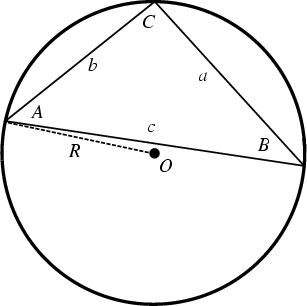
Let ![]() ,
, ![]() , and
, and ![]() be the lengths of the Legs of a Triangle opposite Angles
be the lengths of the Legs of a Triangle opposite Angles ![]() ,
, ![]() , and
, and ![]() .
Then the law of sines states that
.
Then the law of sines states that
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The law of sines for oblique Spherical Triangles states that
| (6) |
See also Law of Cosines, Law of Tangents
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 79, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 148, 1987.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 1-3, 1967.