|
|
|
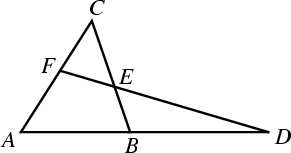
| (1) |
| (2) |
![\begin{displaymath}
\prod_{i=1}^n \left[{V_iW_i\over W_iV_{i+1}}\right]=(-1)^n.
\end{displaymath}](m_928.gif) |
(3) |
| (4) |
See also Ceva's Theorem, Hoehn's Theorem, Pasch's Axiom
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 122, 1987.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 66-67, 1967.
Grünbaum, B. and Shepard, G. C. ``Ceva, Menelaus, and the Area Principle.'' Math. Mag. 68, 254-268, 1995.
Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., p. xxi, 1995.