Ceva's Theorem

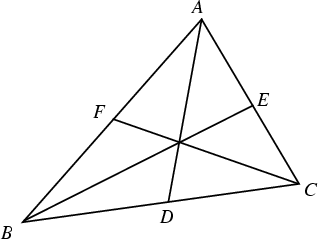
Given a Triangle with Vertices $A$, $B$, and $C$ and points along the sides $D$, $E$, and $F$, a Necessary and Sufficient condition for the Cevians $AD$, $BE$, and $CF$ to be Concurrent (intersect in a single point) is that

$$BD\cdot CE\cdot AF=DC\cdot EA\cdot FB.$$ (1)

Let $P=[V_1, \dots, V_n]$ be an arbitrary $n$-gon, $C$ a given point, and $k$ a Positive Integer such that $1\leq k \leq n/2$. For $i=1$, ..., $n$, let $W_i$ be the intersection of the lines $CV_i$ and $V_{i-k}V_{i+k}$, then

$$\prod_{i=1}^n\left[{V_{i-k}W_i\over W_iV_{i+k}}\right]=1.$$ (2)

Here, $AB\vert\vert CD$ and

$$\left[{AB\over CD}\right]$$ (3)

is the Ratio of the lengths $[A, B]$ and $[C, D]$ with a plus or minus sign depending on whether these segments have the same or opposite directions (Grünbaum and Shepard 1995).

Another form of the theorem is that three Concurrent lines from the Vertices of a Triangle divide the opposite sides in such fashion that the product of three nonadjacent segments equals the product of the other three (Johnson 1929, p. 147).

See also Hoehn's Theorem, Menelaus' Theorem

References

Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 122, 1987.

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 4-5, 1967.

Grünbaum, B. and Shepard, G. C. ``Ceva, Menelaus, and the Area Principle.'' Math. Mag. 68, 254-268, 1995.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 145-151, 1929.

Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., p. xx, 1995.