Brocard Circle

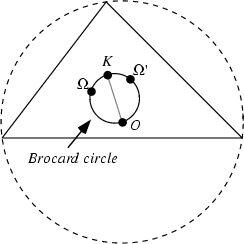
The Circle passing through the first and second Brocard Points $\Omega$ and $\Omega'$, the Lemoine Point $K$, and the Circumcenter $O$ of a given Triangle. The Brocard Points $\Omega$ and $\Omega'$ are symmetrical about the Line ${\leftrightarrow\atop{\displaystyle KO}}$, which is called the Brocard Line. The Line Segment $\overline{KO}$ is called the Brocard Diameter, and it has length

$$\overline{OK}={\overline{O\Omega}\over\cos\omega}={R\sqrt{1-4\sin^2\omega}\over\cos\omega}\,,$$

where $R$ is the Circumradius and $\omega$ is the Brocard Angle. The distance between either of the Brocard Points and the Lemoine Point is

$$\overline{\Omega K}=\overline{\Omega'K}=\overline{\Omega O}\tan\omega.$$

See also Brocard Angle, Brocard Diameter, Brocard Points

References

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, p. 272, 1929.