Kiepert's Parabola

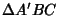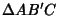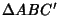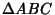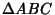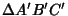Let three similar Isosceles Triangles $\Delta A'BC$, $\Delta AB'C$, and $\Delta ABC'$ be constructed on the sides of a Triangle $\Delta ABC$. Then the Envelope of the axis of the Triangles $\Delta ABC$ and $\Delta A'B'C'$ is Kiepert's parabola, given by

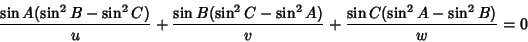$${\sin A(\sin^2 B-\sin^2 C)\over u}+{\sin B(\sin^2 C-\sin^2 A)\over v}+{\sin C(\sin^2 A-\sin^2 B)\over w}=0$$ (1)

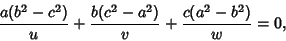$${a(b^2-c^2)\over u}+{b(c^2-a^2)\over v}+{c(a^2-b^2)\over w}=0,$$ (2)

where $[u, v, w]$ are the Trilinear Coordinates for a line tangent to the parabola. It is tangent to the sides of the Triangle, the line at infinity, and the Lemoine Line. The Focus has Triangle Center Function

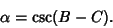$$\alpha=\csc(B-C).$$ (3)

The Euler Line of a triangle is the Directrix of Kiepert's parabola. In fact, the Directrices of all parabolas inscribed in a Triangle pass through the Orthocenter. The Brianchon Point for Kiepert's parabola is the Steiner Point.

See also Brianchon Point, Envelope, Euler Line, Isosceles Triangle, Lemoine Line, Steiner Points