|
|
|
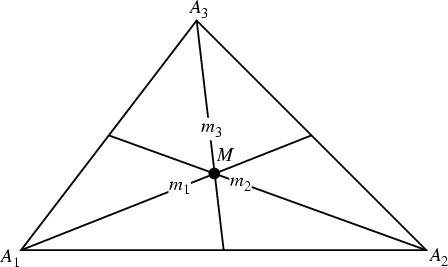
The Cevian from a Triangle's Vertex to the Midpoint of the opposite side is
called a median of the Triangle. The three medians of any Triangle are Concurrent, meeting in the
Triangle's Centroid (which has Trilinear Coordinates ![]() ). In
addition, the medians of a Triangle divide one another in the ratio 2:1. A median also bisects the Area of a
Triangle.
). In
addition, the medians of a Triangle divide one another in the ratio 2:1. A median also bisects the Area of a
Triangle.
Let ![]() denote the length of the median of the
denote the length of the median of the ![]() th side
th side ![]() . Then
. Then
| (1) | |||
| (2) |
| (3) |
| (4) |
A median triangle is a Triangle whose sides are equal and Parallel to the medians of a given Triangle. The median triangle of the median triangle is similar to the given Triangle in the ratio 3/4.
See also Bimedian, Exmedian, Exmedian Point, Heronian Triangle, Medial Triangle
References
Casey, J. A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 5th ed., rev. enl.
Dublin: Hodges, Figgis, & Co., 1888.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 7-8, 1967.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 68, 173-175, 282-283, 1929.
|
|
|
© 1996-9 Eric W. Weisstein