The Gaussian probability distribution with Mean 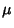 and Standard Deviation
and Standard Deviation 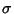 is a Gaussian
Function of the form
is a Gaussian
Function of the form
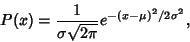 |
(1) |
where 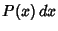 gives the probability that a variate with a Gaussian distribution takes on a value in the range
gives the probability that a variate with a Gaussian distribution takes on a value in the range ![$[x,x+dx]$](g_701.gif) . This distribution
is also called the Normal Distribution or, because of its curved flaring shape, the Bell Curve. The
distribution
. This distribution
is also called the Normal Distribution or, because of its curved flaring shape, the Bell Curve. The
distribution 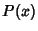 is properly normalized for
is properly normalized for
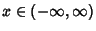 since
since
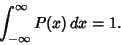 |
(2) |
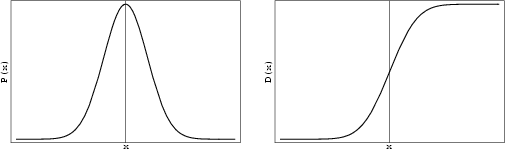
The cumulative Distribution Function, which gives the probability that a variate will assume a value
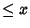 , is then
, is then
 |
(3) |
Gaussian distributions have many convenient properties, so random variates with unknown distributions are often assumed
to be Gaussian, especially in physics and astronomy. Although this can be a dangerous assumption, it is often a good
approximation due to a surprising result known as the Central Limit Theorem. This theorem states that the
Mean of any set of variates with any distribution having a finite Mean and Variance tends to the
Gaussian distribution. Many common attributes such as test scores, height, etc., follow roughly Gaussian distributions,
with few members at the high and low ends and many in the middle.
Making the transformation
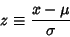 |
(4) |
so that 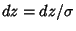 gives a variate with unit Variance and 0 Mean
gives a variate with unit Variance and 0 Mean
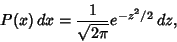 |
(5) |
known as a standard Normal Distribution. So defined, 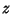 is known as a z-Score.
is known as a z-Score.
The Normal Distribution Function gives the probability that a standard normal variate assumes a value in the interval
![$[0,z]$](g_710.gif) ,
,
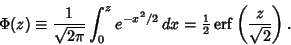 |
(6) |
Here, Erf is a function sometimes called the error function. Neither 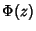 nor Erf can be expressed in terms
of finite additions, subtractions, multiplications, and root extractions, and so both must be either computed numerically or
otherwise approximated. The value of
nor Erf can be expressed in terms
of finite additions, subtractions, multiplications, and root extractions, and so both must be either computed numerically or
otherwise approximated. The value of 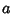 for which
for which 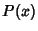 falls within the interval
falls within the interval ![$[-a, a]$](g_713.gif) with a given probability
with a given probability 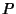 is
called the
is
called the 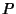 Confidence Interval.
Confidence Interval.
The Gaussian distribution is also a special case of the Chi-Squared Distribution, since substituting
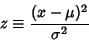 |
(7) |
so that
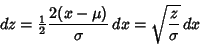 |
(8) |
(where an extra factor of 1/2 has been added to 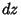 since
since 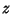 runs from 0 to
runs from 0 to 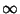 instead of from
instead of from 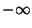 to
to 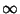 ), gives
), gives
which is a Chi-Squared Distribution in 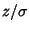 with
with  (i.e., a Gamma Distribution with
(i.e., a Gamma Distribution with 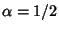 and
and 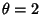 ).
).
Cramer showed in 1936 that if 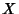 and
and 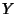 are Independent variates and
are Independent variates and 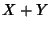 has a
Gaussian distribution, then both
has a
Gaussian distribution, then both 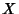 and
and 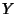 must be Gaussian (Cramer's Theorem).
must be Gaussian (Cramer's Theorem).
The ratio 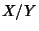 of independent Gaussian-distributed variates with zero Mean is distributed with a Cauchy
Distribution. This can be seen as follows. Let
of independent Gaussian-distributed variates with zero Mean is distributed with a Cauchy
Distribution. This can be seen as follows. Let 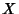 and
and 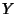 both have Mean 0 and standard deviations of
both have Mean 0 and standard deviations of 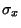 and
and
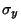 , respectively, then the joint probability density function is the Gaussian Bivariate Distribution with
, respectively, then the joint probability density function is the Gaussian Bivariate Distribution with
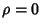 ,
,
![\begin{displaymath}
f(x,y)={1\over 2\pi\sigma_x\sigma_y} e^{-[x^2/(2{\sigma_x}^2)+y^2/(2{\sigma_y}^2)]}.
\end{displaymath}](g_730.gif) |
(10) |
From Ratio Distribution, the distribution of 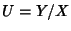 is
is
But
![\begin{displaymath}
\int_0^\infty xe^{-ax^2}\,dx =\left[{-{1\over 2a} e^{-ax^2}}\right]_0^\infty={1\over 2a}[0-(-1)] = {1\over 2a},
\end{displaymath}](g_736.gif) |
(12) |
so
which is a Cauchy Distribution with Mean 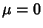 and full width
and full width
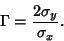 |
(14) |
The Characteristic Function for the Gaussian distribution is
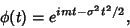 |
(15) |
and the Moment-Generating Function is
Completing the Square in the exponent,
![\begin{displaymath}
{1\over 2\sigma^2} [x^2-2(\mu +\sigma^2t)x+\mu^2]= {1\over 2...
...\{{[x-(\mu +\sigma^2t)]^2+[\mu^2-(\mu +\sigma^2t)^2]}\right\}.
\end{displaymath}](g_744.gif) |
(17) |
Let
The integral then becomes
so
and
These can also be computed using
yielding, as before,
The moments can also be computed directly by computing the Moments about the origin
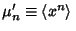 ,
,
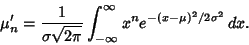 |
(31) |
Now let
giving
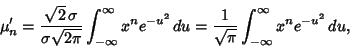 |
(35) |
so
where 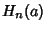 are Gaussian Integrals.
are Gaussian Integrals.
Now find the Moments about the Mean,
so the Variance, Standard Deviation, Skewness, and Kurtosis are given by
The Variance of the Sample Variance 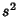 for a sample taken from a population with a Gaussian distribution is
for a sample taken from a population with a Gaussian distribution is
If 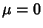 , this expression simplifies to
, this expression simplifies to
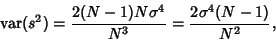 |
(50) |
and the Standard Error is
![\begin{displaymath}
\hbox{[standard error]}={\sqrt{2(N-1)}\over N}.
\end{displaymath}](g_813.gif) |
(51) |
The Cumulant-Generating Function for a Gaussian distribution is
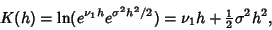 |
(52) |
so
For Gaussian variates, 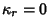 for
for 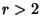 , so the variance of k-Statistic
, so the variance of k-Statistic 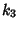 is
is
Also,
where
If 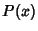 is a Gaussian distribution, then
is a Gaussian distribution, then
![\begin{displaymath}
D(x)={1\over 2}\left[{1+\mathop{\rm erf}\nolimits \left({x-\mu\over \sigma\sqrt{2}}\right)}\right],
\end{displaymath}](g_836.gif) |
(62) |
so variates 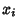 with a Gaussian distribution can be generated from variates
with a Gaussian distribution can be generated from variates 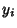 having a Uniform Distribution in
(0,1) via
having a Uniform Distribution in
(0,1) via
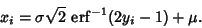 |
(63) |
However, a simpler way to obtain numbers with a Gaussian distribution is to use the Box-Muller Transformation.
The Gaussian distribution is an approximation to the Binomial Distribution in the limit of large numbers,
![\begin{displaymath}
P(n_1) = {1\over\sqrt{ 2\pi Npq}}\,\, \mathop{\rm exp}\nolimits \left[{-{(n_1-Np)^2\over 2Npq}}\right],
\end{displaymath}](g_840.gif) |
(64) |
where 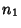 is the number of steps in the Positive direction,
is the number of steps in the Positive direction, 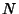 is the number of trials (
is the number of trials (
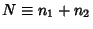 ), and
), and 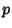 and
and 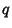 are the probabilities of a step in the Positive direction and Negative direction (
are the probabilities of a step in the Positive direction and Negative direction (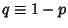 ).
).
The differential equation having a Gaussian distribution as its solution is
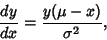 |
(65) |
since
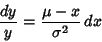 |
(66) |
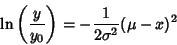 |
(67) |
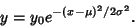 |
(68) |
This equation has been generalized to yield more complicated distributions which are named using the so-called Pearson
System.
See also Binomial Distribution, Central Limit Theorem, Erf, Gaussian Bivariate Distribution,
Logit Transformation, Normal Distribution, Normal Distribution Function, Pearson System,
Ratio Distribution, z-Score
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 533-534, 1987.
Kraitchik, M. ``The Error Curve.'' §6.4 in Mathematical Recreations. New York: W. W. Norton,
pp. 121-123, 1942.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 109-111, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and Standard Deviation
and Standard Deviation ![]() is a Gaussian
Function of the form
is a Gaussian
Function of the form
![]() ,
,
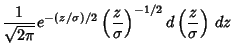

![]() and
and ![]() are Independent variates and
are Independent variates and ![]() has a
Gaussian distribution, then both
has a
Gaussian distribution, then both ![]() and
and ![]() must be Gaussian (Cramer's Theorem).
must be Gaussian (Cramer's Theorem).
![]() of independent Gaussian-distributed variates with zero Mean is distributed with a Cauchy
Distribution. This can be seen as follows. Let
of independent Gaussian-distributed variates with zero Mean is distributed with a Cauchy
Distribution. This can be seen as follows. Let ![]() and
and ![]() both have Mean 0 and standard deviations of
both have Mean 0 and standard deviations of ![]() and
and
![]() , respectively, then the joint probability density function is the Gaussian Bivariate Distribution with
, respectively, then the joint probability density function is the Gaussian Bivariate Distribution with
![]() ,
,
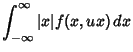
![$\displaystyle {1\over 2\pi\sigma_x\sigma_y} \int_{-\infty}^\infty \vert x\vert e^{-[x^2/(2{\sigma_x}^2)+u^2 x^2/(2{\sigma_y}^2)]}$](g_734.gif)
![$\displaystyle {1\over\pi\sigma_x\sigma_y} \int_0^\infty x\mathop{\rm exp}\nolim...
...-x^2\left({{1\over 2{\sigma_x}^2}+{u^2\over 2{\sigma_y}^2}}\right)}\right]\,dx.$](g_735.gif)
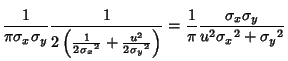
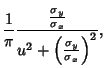
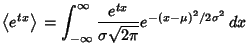
![$\displaystyle {1\over \sigma \sqrt{2\pi}} \int_{-\infty}^\infty \!\mathop{\rm e...
...{- {1\over 2\sigma^2} \left[{x^2-2(\mu +\sigma^2t)x+\mu^2}\right]}\right\}\,dx.$](g_743.gif)
![$\displaystyle {1\over\sigma\sqrt{ 2\pi}} \int_{-\infty}^\infty \mathop{\rm exp}\nolimits \left[{-ay^2 + {2\mu\sigma^2t+\sigma^4t^2\over 2\sigma^2}}\right]\,dy$](g_749.gif)
![$\displaystyle {1\over\sigma\sqrt{2\pi}} \int_{-\infty}^\infty \mathop{\rm exp}\nolimits [-ay^2+\mu t+{\textstyle{1\over 2}}\sigma^2 t^2]\,dy$](g_750.gif)
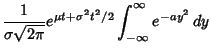
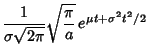
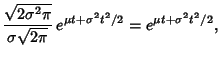
![]() ,
,
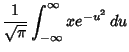
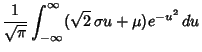
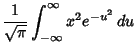
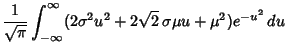
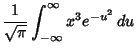
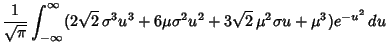
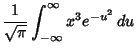
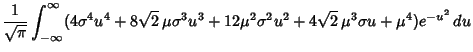
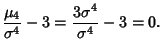
![]() for a sample taken from a population with a Gaussian distribution is
for a sample taken from a population with a Gaussian distribution is
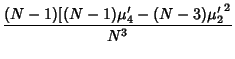
![$\displaystyle {(N-1)\over N^3} [(N-1)(\mu^4+6\mu^2\sigma^2+3\sigma^4)-(N-3)(\mu^2+\sigma^2)^2]$](g_810.gif)
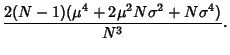
![]() for
for ![]() , so the variance of k-Statistic
, so the variance of k-Statistic ![]() is
is
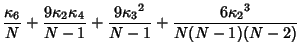
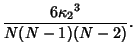
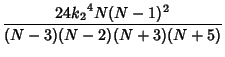
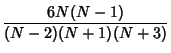
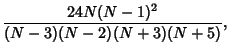
![]() is a Gaussian distribution, then
is a Gaussian distribution, then