The Gaussian bivariate distribution is given by
![\begin{displaymath}
P(x_1,x_2) = {1\over 2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\, \mathop{\rm exp}\nolimits \left[{-{z\over 2(1-\rho^2)}}\right],
\end{displaymath}](g_528.gif) |
(1) |
where
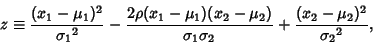 |
(2) |
and
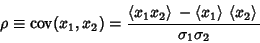 |
(3) |
is the Covariance. Let 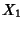 and
and 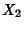 be normally and independently distributed variates with Mean 0 and
Variance 1. Then define
be normally and independently distributed variates with Mean 0 and
Variance 1. Then define
These new variates are normally distributed with Mean 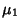 and
and 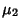 , Variance
, Variance
and Covariance
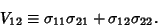 |
(8) |
The Covariance matrix is
![\begin{displaymath}
V_{ij} = \left[{\matrix{{\sigma_1}^2 & \rho\sigma_1\sigma_2\cr \rho\sigma_1\sigma_2 & {\sigma_2}^2\cr}}\right],
\end{displaymath}](g_542.gif) |
(9) |
where
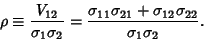 |
(10) |
The joint probability density function for 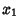 and
and 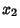 is
is
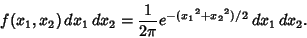 |
(11) |
However, from (4) and (5) we have
![\begin{displaymath}
\left[{\matrix{y_1-\mu_1\cr y_2-\mu_2\cr}}\right] = \left[{\...
...\sigma_{22}\cr}}\right] \left[{\matrix{x_1\cr x_2\cr}}\right].
\end{displaymath}](g_547.gif) |
(12) |
Now, if
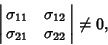 |
(13) |
then this can be inverted to give
Therefore,
![\begin{displaymath}
{x_1}^2+{x_2}^2 = {[\sigma_{22}(y_1-\mu_1)-\sigma_{12}(y_2-\...
..._2)]^2\over(\sigma_{11}\sigma_{22}-\sigma_{12}\sigma_{21})^2}.
\end{displaymath}](g_552.gif) |
(15) |
Expanding the Numerator gives
so
But
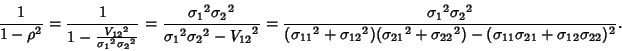 |
(18) |
The Denominator is
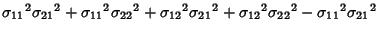
|
|
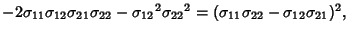
|
(19) |
so
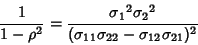 |
(20) |
and
![\begin{displaymath}
{x_1}^2+{x_2}^2={1\over 1-\rho^2}\left[{{(y_1-\mu_1)^2\over ...
...r \sigma_1\sigma_2}+{(y_2-\mu_2)^2\over {\sigma_2}^2}}\right].
\end{displaymath}](g_565.gif) |
(21) |
Solving for 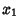 and
and 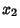 and defining
and defining
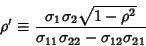 |
(22) |
gives
The Jacobian is
Therefore,
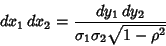 |
(26) |
and
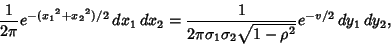 |
(27) |
where
![\begin{displaymath}
v\equiv {1\over 1-\rho^2}\left[{{(y_1-\mu_1)^2\over{\sigma_1...
...er\sigma_1\sigma_2}+{(y_2-\mu_2)^2\over {\sigma_2}^2}}\right].
\end{displaymath}](g_577.gif) |
(28) |
Now, if
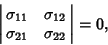 |
(29) |
then
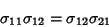 |
(30) |
so
where
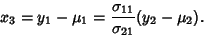 |
(35) |
The Characteristic Function is given by
where
![\begin{displaymath}
z\equiv \left[{{(x_1-\mu_1)^2\over{\sigma_1}^2}} {-{2\rho(x_...
...ver\sigma_1\sigma_2}+{(x_2-\mu_2)^2\over {\sigma_2}^2}}\right]
\end{displaymath}](g_591.gif) |
(37) |
and
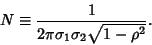 |
(38) |
Now let
Then
![\begin{displaymath}
\phi(t_1,t_2) = N'\int_{-\infty}^\infty \left({e^{it_2w} \ma...
...^2}}\right]}\right)\int_{-\infty}^\infty e^v e^{t_1u}\,du\,dw,
\end{displaymath}](g_597.gif) |
(41) |
where
Complete the Square in the inner integral
![$\int_{-\infty}^\infty \mathop{\rm exp}\nolimits \left\{{-{1\over 2(1-\rho^2)}{1...
...1}^2}\left[{{u}^2-{2\rho\sigma_1w\over\sigma_2} u}\right]}\right\} e^{t_1u}\,du$](g_602.gif)
|
|
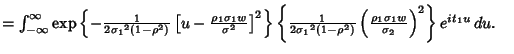
|
(43) |
Rearranging to bring the exponential depending on 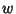 outside the inner integral, letting
outside the inner integral, letting
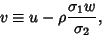 |
(44) |
and writing
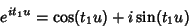 |
(45) |
gives
Expanding the term in braces gives
But
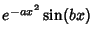 is Odd, so the integral over the sine term vanishes, and we are left with
is Odd, so the integral over the sine term vanishes, and we are left with
Now evaluate the Gaussian Integral
to obtain the explicit form of the Characteristic Function,
Let 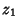 and
and 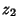 be two independent Gaussian variables with Means
be two independent Gaussian variables with Means 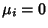 and
and
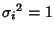 for
for 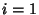 ,
2. Then the variables
,
2. Then the variables 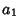 and
and 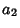 defined below are Gaussian bivariates with unit Variance and
Cross-Correlation Coefficient
defined below are Gaussian bivariates with unit Variance and
Cross-Correlation Coefficient 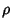 :
:
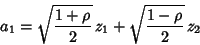 |
(51) |
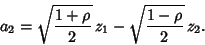 |
(52) |
The conditional distribution is
![\begin{displaymath}
P(x_2\vert x_1) = {1\over \sigma_2\sqrt{2\pi(1-\rho^2)}}\mat...
...limits \left[{- { (x^2-\mu'^2)^2\over 2{\sigma_2'}^2}}\right],
\end{displaymath}](g_635.gif) |
(53) |
where
The marginal probability density is
See also Box-Muller Transformation, Gaussian Distribution, McMohan's Theorem,
Normal Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 936-937, 1972.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 118, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![$\displaystyle \left[\begin{array}{cc}\sigma_{11} & \sigma_{12}\\ \sigma_{21} &...
...t]^{-1}
\left[\begin{array}{c}y_1-\mu_1\\ y_2-\mu_2\end{array}\right]\nonumber$](g_550.gif)
![$\displaystyle {1\over \sigma_{11}\sigma_{22}-\sigma_{12}\sigma_{21}}
\left[\beg...
...right]
\left[\begin{array}{c}y_1-\mu_1\\ y_2-\mu_2\end{array}\right].\nonumber$](g_551.gif)
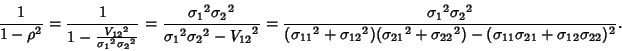
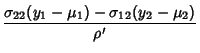
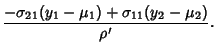
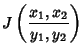
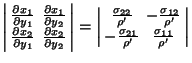
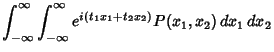
![$\displaystyle N \int_{-\infty}^\infty \int_{-\infty}^\infty e^{i(t_1x_1+t_2x_2)} \mathop{\rm exp}\nolimits \left[{-{z\over 2(1-\rho^2)}}\right]\,dx_1\,dx_2,$](g_590.gif)
![$\displaystyle -{1\over 2(1-\rho^2)} {1\over {\sigma_1}^2} \left[{{u}^2-{2\rho\sigma_1w\over \sigma_2} u}\right]$](g_599.gif)
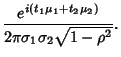
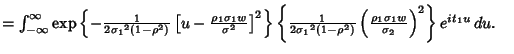
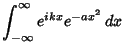
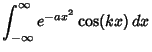
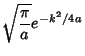
![$\phi(t_1,t_2) = {e^{i(t_1\mu_1+t_2\mu_2)}\over 2\pi\sigma_1\sigma_2\sqrt{1-\rho...
...ft({t_2+\rho{\sigma_1\over\sigma_2}t_1}\right)^2 2{\sigma_2}^2}\right]}\right\}$](g_621.gif)
![]() and
and ![]() be two independent Gaussian variables with Means
be two independent Gaussian variables with Means ![]() and
and
![]() for
for ![]() ,
2. Then the variables
,
2. Then the variables ![]() and
and ![]() defined below are Gaussian bivariates with unit Variance and
Cross-Correlation Coefficient
defined below are Gaussian bivariates with unit Variance and
Cross-Correlation Coefficient ![]() :
:
![\begin{displaymath}
P(x_2\vert x_1) = {1\over \sigma_2\sqrt{2\pi(1-\rho^2)}}\mat...
...limits \left[{- { (x^2-\mu'^2)^2\over 2{\sigma_2'}^2}}\right],
\end{displaymath}](g_635.gif)
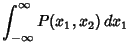
![$\displaystyle {1\over\sigma_2\sqrt 2\pi}\mathop{\rm exp}\nolimits \left[{-{(x_2-\mu_2)^2\over 2{\sigma_2}^2}}\right].$](g_642.gif)