|
|
|
The characteristic function ![]() is defined as the Fourier Transform of the Probability Density Function,
is defined as the Fourier Transform of the Probability Density Function,
![$\displaystyle {\mathcal F}[P(x)] = \int_{-\infty}^\infty e^{itx}P(x)\, dx$](c1_1235.gif) |
(1) | ||
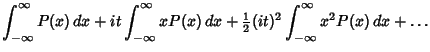 |
(2) | ||
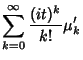 |
(3) | ||
| (4) |
| (5) |
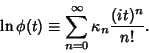 |
(6) |
A Distribution is not uniquely specified by its Moments, but is uniquely specified by its characteristic function.
See also Cumulant, Moment, Moment-Generating Function, Probability Density Function
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 928, 1972.
Kenney, J. F. and Keeping, E. S. ``Moment-Generating and Characteristic Functions,'' ``Some Examples of Moment-Generating Functions,''
and ``Uniqueness Theorem for Characteristic Functions.'' §4.6-4.8 in Mathematics of Statistics, Pt. 2, 2nd ed.
Princeton, NJ: Van Nostrand, pp. 72-77, 1951.