|
|
|
Let ![]() be the Characteristic Function, defined as the Fourier Transform of the
Probability Density Function,
be the Characteristic Function, defined as the Fourier Transform of the
Probability Density Function,
| (1) |
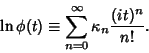 |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) |
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) |
The k-Statistic are Unbiased Estimators of the cumulants.
See also Characteristic Function, Cumulant-Generating Function, k-Statistic, Kurtosis, Mean, Moment, Sheppard's Correction, Skewness, Variance
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 928, 1972.
Kenney, J. F. and Keeping, E. S. ``Cumulants and the Cumulant-Generating Function,'' ``Additive Property of Cumulants,''
and ``Sheppard's Correction.'' §4.10-4.12 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 77-82, 1951.
|
|
|
© 1996-9 Eric W. Weisstein