|
|
|
For a Field ![]() with multiplicative identity 1, consider the numbers
with multiplicative identity 1, consider the numbers ![]() ,
, ![]() ,
, ![]() , etc. Either
these numbers are all different, in which case we say that
, etc. Either
these numbers are all different, in which case we say that ![]() has characteristic 0, or two of them will be equal. In
this case, it is straightforward to show that, for some number
has characteristic 0, or two of them will be equal. In
this case, it is straightforward to show that, for some number ![]() , we have
, we have
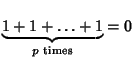 . If
. If ![]() is chosen to be as small as possible, then
is chosen to be as small as possible, then ![]() will be a Prime, and we say that
will be a Prime, and we say that ![]() has
characteristic
has
characteristic ![]() . The Fields
. The Fields ![]() ,
, ![]() ,
, ![]() , and the p-adic Number
, and the p-adic Number ![]() have characteristic 0. For
have characteristic 0. For ![]() a Prime,
the Galois Field GF(
a Prime,
the Galois Field GF(![]() ) has characteristic
) has characteristic ![]() .
.
If ![]() is a Subfield of
is a Subfield of ![]() , then
, then ![]() and
and ![]() have the same characteristic.
have the same characteristic.
See also Field, Subfield