Another name for a Gaussian Distribution. Given a normal distribution in a Variate 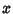 with Mean
with Mean
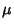 and Variance
and Variance 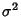 ,
,
the so-called ``Standard Normal Distribution'' is given by taking 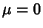 and
and 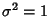 . An arbitrary normal
distribution can be converted to a Standard Normal Distribution by changing variables to
. An arbitrary normal
distribution can be converted to a Standard Normal Distribution by changing variables to
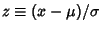 , so
, so
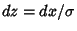 , yielding
, yielding
The Fisher-Behrens Problem is the determination of a test for the equality of Means for two normal
distributions with different Variances.
See also Fisher-Behrens Problem, Gaussian Distribution, Half-Normal Distribution, Kolmogorov-Smirnov
Test, Normal Distribution Function, Standard Normal Distribution, Tetrachoric Function
© 1996-9 Eric W. Weisstein
1999-05-25
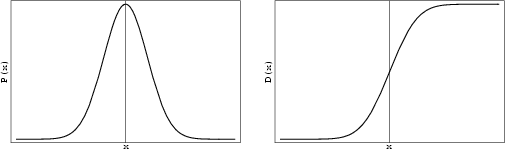
![]() with Mean
with Mean
![]() and Variance
and Variance ![]() ,
,