|
|
|
A transformation which transforms from a 2-D continuous Uniform Distribution to a 2-D Gaussian Bivariate
Distribution (or Complex Gaussian Distribution). If ![]() and
and ![]() are uniformly and
independently distributed between 0 and 1, then
are uniformly and
independently distributed between 0 and 1, then ![]() and
and ![]() as defined below have a Gaussian Distribution with
Mean
as defined below have a Gaussian Distribution with
Mean ![]() and Variance
and Variance ![]() .
.
| (1) | |||
| (2) |
| (3) | |||
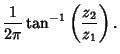 |
(4) |
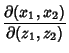 |
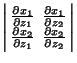 |
||
![$\displaystyle -\left[{{1\over\sqrt{2\pi}}e^{-{z_1}^2/2}}\right]\left[{{1\over\sqrt{2\pi}}e^{-{z_2}^2/2}}\right].$](b_1970.gif) |
(5) |