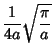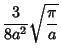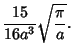The Gaussian integral, also called the Probability Integral, is the integral of the 1-D Gaussian over
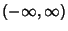 . It can be computed using the trick of combining two 1-D Gaussians
. It can be computed using the trick of combining two 1-D Gaussians
and switching to Polar Coordinates,
However, a simple proof can also be given which does not require transformation to Polar Coordinates (Nicholas and
Yates 1950).
The integral from 0 to a finite upper limit 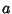 can be given by the
Continued Fraction
can be given by the
Continued Fraction
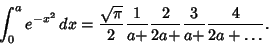 |
(3) |
The general class of integrals of the form
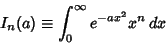 |
(4) |
can be solved analytically by setting
Then
For 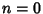 , this is just the usual Gaussian integral, so
, this is just the usual Gaussian integral, so
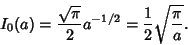 |
(9) |
For 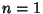 , the integrand is integrable by quadrature,
, the integrand is integrable by quadrature,
![\begin{displaymath}
I_1(a)= a^{-1} \int_0^\infty e^{-y^2}y\,dy = a^{-1}[-{\textstyle{1\over 2}}e^{-y^2}]^\infty_0 = {\textstyle{1\over 2}}a^{-1}.
\end{displaymath}](g_929.gif) |
(10) |
To compute 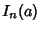 for
for 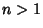 , use the identity
, use the identity
For 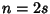 Even,
Even,
so
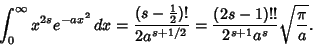 |
(13) |
If 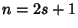 is Odd, then
is Odd, then
so
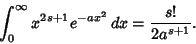 |
(15) |
The solution is therefore
![\begin{displaymath}
\int_0^\infty e^{-ax^2}x^n\,dx =\cases{
{(n-1)!!\over 2^{n/...
...$\ even\cr
{[(n+1)/2]!\over 2a^{(n+1)/2}} & for $n$\ odd.\cr}
\end{displaymath}](g_946.gif) |
(16) |
The first few values are therefore
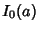 |
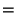 |
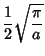 |
(17) |
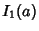 |
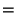 |
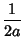 |
(18) |
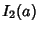 |
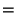 |
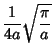 |
(19) |
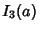 |
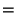 |
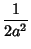 |
(20) |
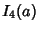 |
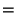 |
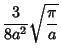 |
(21) |
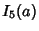 |
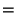 |
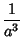 |
(22) |
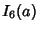 |
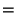 |
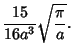 |
(23) |
A related, often useful integral is
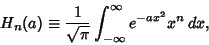 |
(24) |
which is simply given by
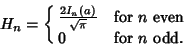 |
(25) |
References
Nicholas, C. B. and Yates, R. C. ``The Probability Integral.'' Amer. Math. Monthly 57, 412-413, 1950.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() . It can be computed using the trick of combining two 1-D Gaussians
. It can be computed using the trick of combining two 1-D Gaussians
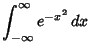
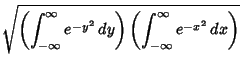
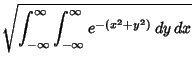
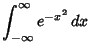
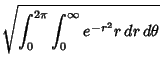
![]() can be given by the
Continued Fraction
can be given by the
Continued Fraction
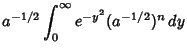
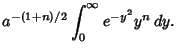
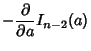
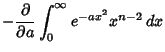
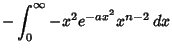
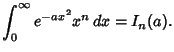
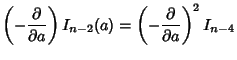
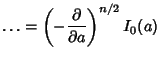
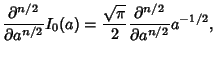
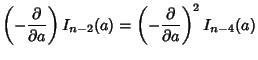
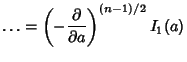
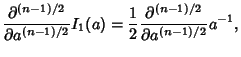
![\begin{displaymath}
\int_0^\infty e^{-ax^2}x^n\,dx =\cases{
{(n-1)!!\over 2^{n/...
...$\ even\cr
{[(n+1)/2]!\over 2a^{(n+1)/2}} & for $n$\ odd.\cr}
\end{displaymath}](g_946.gif)