|
|
|
The standard deviation is defined as the Square Root of the Variance,
| (1) |
| (2) |
The square root of the Sample Variance is the ``sample'' standard deviation,
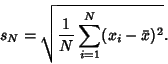 |
(3) |
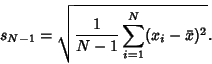 |
(4) |
Physical scientists often use the term Root-Mean-Square as a synonym for standard deviation when they refer to the Square Root of the mean squared deviation of a signal from a given baseline or fit.
See also Mean, Moment, Root-Mean-Square, Sample Variance, Standard Error, Variance