|
|
|
To estimate the population Variance from a sample of ![]() elements with a priori unknown Mean (i.e.,
the Mean is estimated from the sample itself), we need an unbiased Estimator for
elements with a priori unknown Mean (i.e.,
the Mean is estimated from the sample itself), we need an unbiased Estimator for ![]() . This is the
k-Statistic
. This is the
k-Statistic ![]() , where
, where
| (1) |
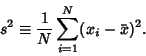 |
(2) |
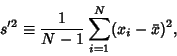 |
(3) |
See also k-Statistic, Variance