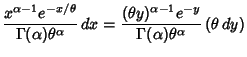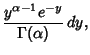A general type of statistical Distribution which is related to the Beta Distribution and arises naturally in
processes for which the waiting times between Poisson Distributed events are relevant. Gamma
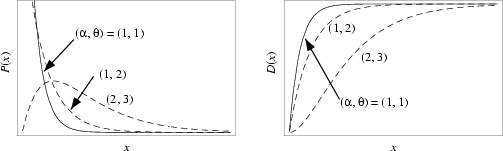
distributions have two free parameters, labeled 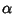 and
and 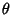 , a few of which are illustrated above.
, a few of which are illustrated above.
Given a Poisson Distribution with a rate of change 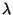 , the Distribution Function
, the Distribution Function 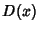 giving the
waiting times until the
giving the
waiting times until the 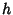 th change is
th change is
for 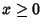 . The probability function
. The probability function 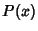 is then obtained by differentiating
is then obtained by differentiating 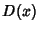 ,
,
Now let
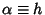 and define
and define
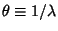 to be the time between changes. Then the above equation
can be written
to be the time between changes. Then the above equation
can be written
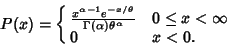 |
(3) |
The Characteristic Function describing this distribution is
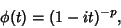 |
(4) |
and the Moment-Generating Function is
In order to find the Moments of the distribution, let
so
and the logarithmic Moment-Generating function is
The Mean, Variance, Skewness, and Kurtosis are then
The gamma distribution is closely related to other statistical distributions.
If 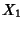 ,
, 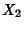 , ...,
, ..., 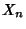 are independent random variates with a gamma distribution having parameters
are independent random variates with a gamma distribution having parameters
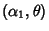 ,
,
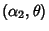 , ...,
, ...,
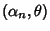 , then
, then
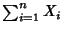 is distributed as gamma with
parameters
is distributed as gamma with
parameters
Also, if 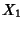 and
and 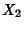 are independent random variates with a gamma distribution having parameters
are independent random variates with a gamma distribution having parameters
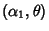 and
and
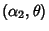 , then
, then 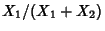 is a Beta Distribution variate with parameters
is a Beta Distribution variate with parameters
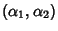 . Both can be derived as follows.
. Both can be derived as follows.
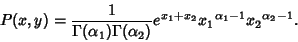 |
(18) |
Let
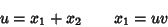 |
(19) |
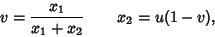 |
(20) |
then the Jacobian is
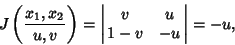 |
(21) |
so
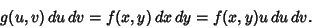 |
(22) |
The sum 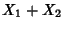 therefore has the distribution
therefore has the distribution
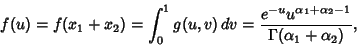 |
(24) |
which is a gamma distribution, and the ratio 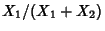 has the distribution
has the distribution
where 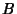 is the Beta Function, which is a Beta Distribution.
is the Beta Function, which is a Beta Distribution.
If 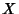 and
and 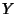 are gamma variates with parameters
are gamma variates with parameters 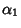 and
and 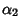 , the
, the 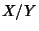 is a variate with a Beta
Prime Distribution with parameters
is a variate with a Beta
Prime Distribution with parameters 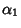 and
and 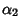 . Let
. Let
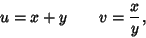 |
(26) |
then the Jacobian is
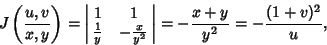 |
(27) |
so
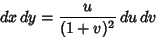 |
(28) |
The ratio 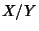 therefore has the distribution
therefore has the distribution
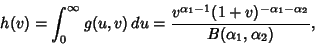 |
(30) |
which is a Beta Prime Distribution with parameters
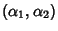 .
.
The ``standard form'' of the gamma distribution is given by letting
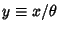 , so
, so 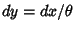 and
and
so the Moments about 0 are
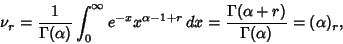 |
(32) |
where 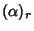 is the Pochhammer Symbol. The Moments about
is the Pochhammer Symbol. The Moments about 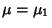 are then
are then
The Moment-Generating Function is
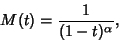 |
(37) |
and the Cumulant-Generating Function is
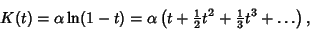 |
(38) |
so the Cumulants are
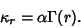 |
(39) |
If 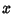 is a Normal variate with Mean
is a Normal variate with Mean 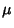 and Standard Deviation
and Standard Deviation 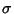 ,
then
,
then
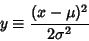 |
(40) |
is a standard gamma variate with parameter  .
.
See also Beta Distribution, Chi-Squared Distribution
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 534, 1987.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
and ![]() , a few of which are illustrated above.
, a few of which are illustrated above.
![]() , the Distribution Function
, the Distribution Function ![]() giving the
waiting times until the
giving the
waiting times until the ![]() th change is
th change is
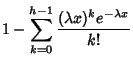
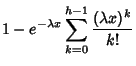
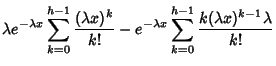
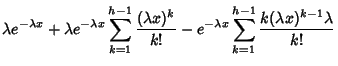
![$\displaystyle \lambda e^{-\lambda x} - \lambda e^{-\lambda x} \sum_{k=1}^{h-1}
\left[{{ k(\lambda x)^{k-1}\over k!} - { (\lambda x)^k\over k!}}\right]$](g_101.gif)
![$\displaystyle \lambda e^{-\lambda x}\left\{{ 1 - \sum_{k=1}^{h-1} \left[{ (\lambda x)^{k-1}\over (k-1)!}
- { (\lambda x)^k\over k!}\right]}\right\}$](g_102.gif)
![$\displaystyle \lambda e^{-\lambda x}\left\{{ 1 - \left[{1 - { (\lambda x)^{h-1}...
...)!}}\right]}\right\}
= { \lambda (\lambda x)^{h-1}\over (h-1)!} e^{-\lambda x}.$](g_103.gif)
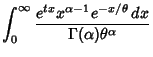
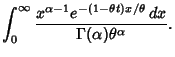
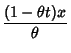
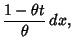
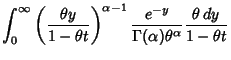
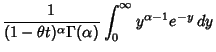
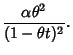
![]() ,
, ![]() , ...,
, ..., ![]() are independent random variates with a gamma distribution having parameters
are independent random variates with a gamma distribution having parameters
![]() ,
,
![]() , ...,
, ...,
![]() , then
, then
![]() is distributed as gamma with
parameters
is distributed as gamma with
parameters
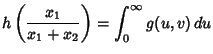
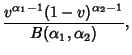
![]() and
and ![]() are gamma variates with parameters
are gamma variates with parameters ![]() and
and ![]() , the
, the ![]() is a variate with a Beta
Prime Distribution with parameters
is a variate with a Beta
Prime Distribution with parameters ![]() and
and ![]() . Let
. Let
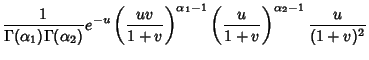
![]() , so
, so ![]() and
and